Our research activities have a focus on the numerical modeling and simulation of fluid dynamic problems in nature and technology. More precisely, we are concerned with
- computational fluid dynamics (CFD) simulations of
- multiphase systems (sprays, gas-solid flows),
- turbulent combustion,
- low-dimensional stochastic modeling of combustion processes and multiphase flows,
- model development for reactive and non-reactive fluid dynamic systems,
- high-performance computing.
More detailed information on our current research is provided below.
Disperse multiphase systems
Dispersed multiphase flows are dynamic systems of two or more phases, at least one of which is dispersed in a fluid in the form of fine particles. Systems of this kind are omnipresent in nature and technology. Weather patterns, ocean currents and blood circulation are just a few examples of their numerous occurrences in nature, while their importance in engineering is illustrated by examples such as drive systems, energy and heat engineering and manufacturing technologies. The numerical modelling of such systems is particularly challenging in terms of the mathematical representation of the disperse phase and the associated physical phenomena such as turbulence and various mechanisms of mass, momentum and energy exchange.
Modelling approaches
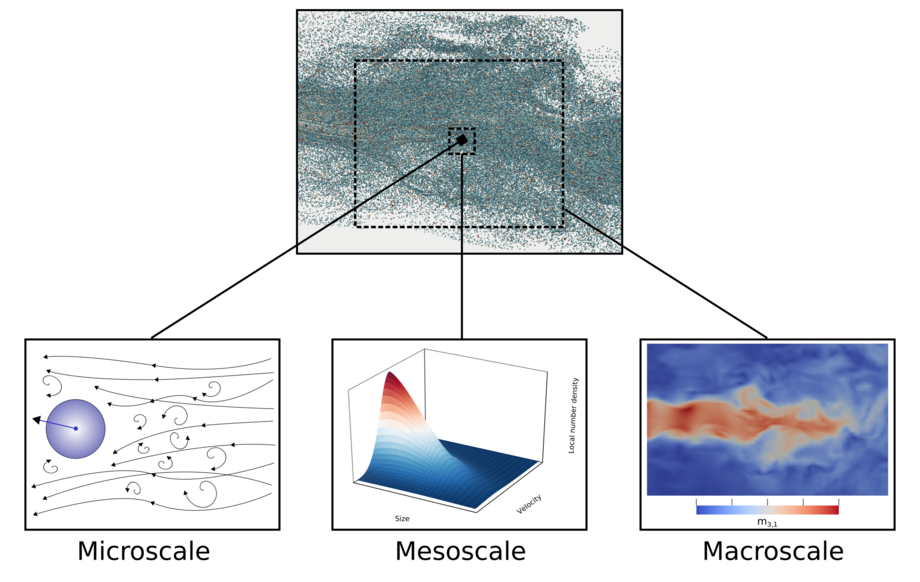
Mathematics representations of the disperse subsystem can be divided into microscopic, mesoscopic or macroscopic modelling approaches:
- Microscopic models capture physical processes down to the particle level. Such approaches are undoubtedly associated with the highest level of detail, but require computing capacities that may be too high for many physical applications.
- Mesoscopic models are aimed at a statistical representation of the local population. This is given in the form of a number density function (NDF), the development of which is described by a population balance equation (PBE).
- Macroscopic models are often advantageous and more efficient, since the target variables of numerical simulations are in many cases macroscopic variables such as concentration, mass, momentum or kinetic energy.
Our research focuses primarily on one particular macroscopic modelling approach, the quadrature-based moment methods (QBMM).
Quadrature-based moment methods
QBMM are based on the macroscopic description in the form of moments of the NDF. The moment equations can be derived directly from the underlying PBE. Taking into account only one internal coordinate \(\xi\) as well as advection and diffusion with the drift function \(\mathcal{A}(\xi)\) and diffusivity \(\mathcal{D}(\xi)\), the NDF \(n\) over time \(t\) follows the equation
\(\frac{\partial n(\xi, t)}{\partial t} = - \frac{\partial }{\partial \xi} \left[ \mathcal{A}(\xi) \, n(\xi, t) \right] \; + \; \frac{\partial^2 }{\partial \xi^2} \left[ \mathcal{D}(\xi) \, n(\xi, t) \right]\).
If the definition of the \(k\)-th moment \(m_k = \int_\Omega \xi^k n(\xi) \mathrm{d} \xi\), the following results for the \(k\)-th moment equation
\(\frac{\mathrm{d} m_k(t)}{\mathrm{d} t} = - k \int_\Omega \xi^{k-1} \, \mathcal{A}(\xi) \, n(\xi, t) \mathrm{d} \xi \; + \; k(k-1) \int_\Omega \xi^{k-2} \, \mathcal{D}(\xi) \, n(\xi, t) \mathrm{d} \xi\).
The moment equations cannot be solved in this form without knowledge of the NDF. QBMM offer a solution to this closure problem by applying quadrature formulas, i.e.
\(\frac{\mathrm{d} m_k(t)}{\mathrm{d} t} \approx - k \sum\limits_j w_j \, \xi_j^{k-1} \, \mathcal{A}(\xi_j) \; + \; k(k-1) \sum\limits_j w_j \, \xi_j^{k-2} \, \mathcal{D}(\xi_j)\).
If the quadrature nodes \(\xi_j\) and weights \(w_j\) are the nodes and weights of the Gaussian quadrature with the weight function \(n\), the method for closing the moment equations is referred to as the quadrature method of moments (QMOM) [1]. This is the basis of numerous derived quadrature methods, see [2]. All these methods have in common that the quadrature formula sought can be calculated exclusively from the known information in the form of moments. As part of our research, we have developed an extension of the QMOM by applying the anti-Gauss quadrature formulas presented by Laurie [3], which in particular should improve the quality of the approximation for strongly nonlinear problems.
Results: Droplet decay
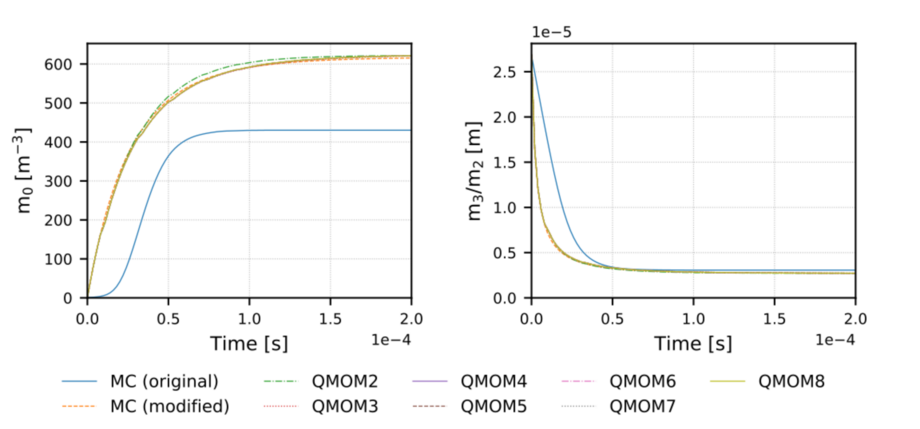
As part of our research activities, we have formulated the moment transport equations for a modified version of the widely used Reitz-Diwakar model for droplet decay [4] and applied the QMOM for closure. Fig. 2 shows the comparison with high-resolution Monte Carlo simulations of the PBE in terms of the total droplet number concentration \(m_0\) and the mean Sauter diameter \(m_3/m_2\). By using the QMOM with more than two quadrature nodes, high accuracy can be achieved at only a fraction of the computational cost.
Results: Turbulence-induced diffusion
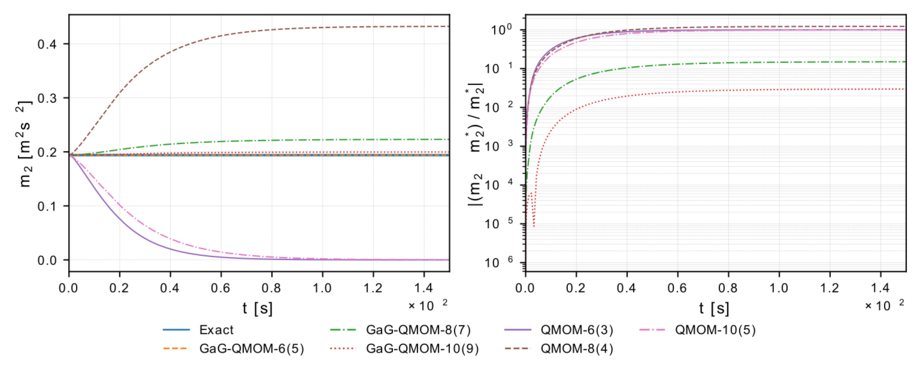
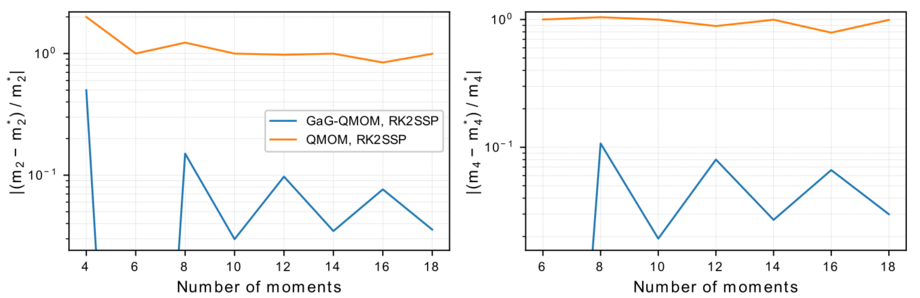
We have applied our extension of QMOM, the Gaussian/anti-Gaussian QMOM (GaG-QMOM), to a spatially homogeneous turbulent system. The strongly non-linear turbulence-induced terms in the PBE pose particular challenges for QBMM. As can be seen in Fig. 3 and Fig. 4, the application of GaG-QMOM leads to a significant increase in accuracy in all cases.
References
| [1] | R. McGraw. Description of aerosol dynamics by the quadrature method of moments. Aerosol Sci. Tech., 27(2):255-265, 1997. |
| [2] | D. L. Marchisio and R. O. Fox. Computational Models for Polydisperse Particulate and Multiphase Systems. Cambridge University Press, 2013. |
| [3] | D. Laurie. Anti-Gaussian quadrature formulas. Math. Comput., 65(214):739-747, 1996. |
| [4] | R. D. Reitz and R. Diwakar. Effect of drop breakup on fuel sprays. SAE Tech. Pap., 860469,1986. |
Overview and aim of the research
In co-operation with the Geophysical Fluid Dynamics working group at the FU Berlin, we are researching the theoretical framework conditions of Shockless Explosion Combustion (SEC), which represents a completely new operating concept for gas turbines. The essential basis of SEC is the controlled homogeneous self-ignition of the fuel, whereby a dynamic approximation to an energetically more favourable constant volume combustion (CVC) is to be achieved. [2] The numerical investigation of the flows occurring here takes place on very small time and length scales, which also requires a considerable effort for the numerical flow solver (Computational Fluid Dynamics, CFD). We are therefore developing our own CFD solver, paying particular attention to efficient numerical methods and parallelisation of the simulations. In the following, we give a rough overview of the numerical methods we use, focussing in particular on adaptive mesh refinement (AMR) methods.
Numerical methods
The general basis for the numerical solution of the problems discussed here are the reactive Euler equations for several species. These are in their three-dimensional conservative form:
\begin{gather}
\frac{\partial \mathbf{U}}{\partial t}
+ \frac{\partial \mathbf{F}(\mathbf{U})}{\partial x}
+ \frac{\partial \mathbf{G}(\mathbf{U})}{\partial y}
+ \frac{\partial \mathbf{H}(\mathbf{U})}{\partial z}
= \mathbf{S}(\mathbf{U}) \,, \label{eq:eulerEquation} \\
\mathbf{U} = \begin{bmatrix}
\rho \\ \rho u \\ \rho v \\ \rho w \\ \rho E \\ \rho Y_s
\end{bmatrix} ,\,
\mathbf{F} = \begin{bmatrix}
\rho u \\ \rho u^2+p \\ \rho uv \\ \rho uw \\ u(\rho E+p) \\ \rho u Y_s
\end{bmatrix} ,\,
\mathbf{G} = \begin{bmatrix}
\rho v \\ \rho uv \\ \rho v^2+p \\ \rho vw \\ v(\rho E+p) \\ \rho v Y_s
\end{bmatrix} ,\,
\mathbf{H} = \begin{bmatrix}
\rho w\\ \rho uw \\ \rho vw \\ \rho w^2+p \\ w(\rho E+p) \\ \rho w Y_s
\end{bmatrix} ,\, \label{eq:eulerComponents}
\end{gather}
where \(\rho\) is the density, \(\mathbf{u}=(u,v,w)\) the velocity, \(E=e+||\mathbf{u}||^2/2\) the total energy, \(e\) the internal energy, \(p\) the pressure and \(Y_s,\,s=1,\ldots,N_s-1\) the mass fractions of the reactive species, which are normalised so that they sum to one. The above equations are closed by the approximation as a calorically perfect gas \(p=\rho(\gamma-1)e\), where \(\gamma=c_p/c_v\) is the ratio of the specific heats. The term \(\mathbf{S}(\mathbf{U})\) is a placeholder for any possible source term that takes into account, for example, external forces, chemical reactions or any supply of mass, momentum, energy or species. To compute the numerical solution of the above equations, we use fully conservative finite volume schemes discretised on block-structured Cartesian grids. Thanks to the use of the external C++ library AMReX [5] in our CFD solver, we can locally refine the grid in the regions of interest using AMR techniques [1]. To ensure the stability of small or irregular cells resulting from the embedding of complex geometries in the structured grids, we use a conservative cut-cell method [3].
Adaptive grid refinement
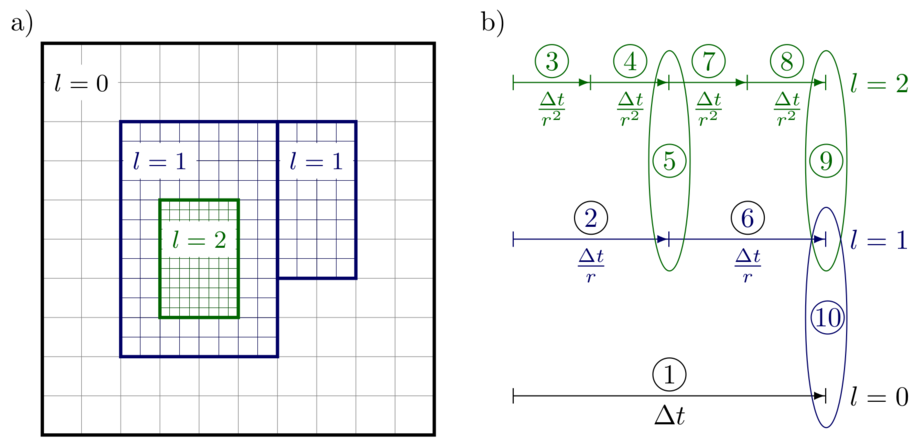
Figure 1 a) shows a simplified sketch of an adaptive Cartesian grid with a total of three planes \((l=0,1,2)\), where the computational domain on each AMR plane is divided into a large number of rectangular regions. The bold lines represent grid boundaries and all cells of each AMR plane \(l_i\) are refined with a refinement ratio \(r\) compared to the plane \(l_{i-1}\). For efficient time integration on adaptive grids, we can use the so-called subcycling-in-time approach [5], where each AMR plane is advanced with its own time step \(\Delta t / r^l\) and synchronisation takes place when the plane \(l_i\) and \(l_{i-1}\) have reached the same time point. This approach is shown in Figure 1 b) as an example for three levels. There are two problems with this approach: (i) The coarse data at level \(l_{i-1}\) is not necessarily equal to the average of the finer data at level \(l_i\). (ii) Due to inconsistent fluxes across the coarse-fine interfaces, the conservation of mass, momentum or energy is violated. Therefore, in each synchronisation step, we must (i) replace the coarse grid data with averaged data from the overlaying fine grid and (ii) perform a flux correction at the coarse-fine interfaces.
Results
Here we present some selected results of simulations to investigate the diffraction of shock waves by non-static media [4]. For these simulations, we consider a one-dimensional pipe through which a given mass flow passes and in which a shock is implemented after a certain time. The pipe is followed by a two-dimensional plenum in which the shock is diffracted. Here we restrict the simulations to two dimensions, no species and add an additional geometric source term:
\begin{equation}
\mathbf{S}(\mathbf{U}) = - \frac{1}{y} \begin{bmatrix}
\rho v ,& \rho uv ,& \rho v^2 ,& v(\rho E+p)
\end{bmatrix}^\text{T},
\end{equation}
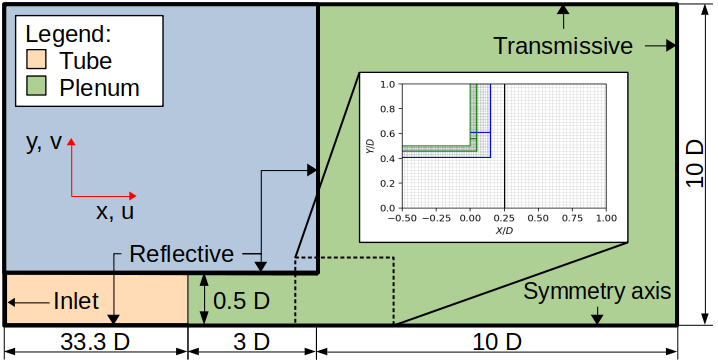
which takes into account the cylindrical symmetry around the \(x\)-axis. A sketch of our simulation domain with boundary conditions (BC's) is shown in Figure 2, where the inset figure shows details of the embedded plenum in the structured adaptive grid with a total of three levels.
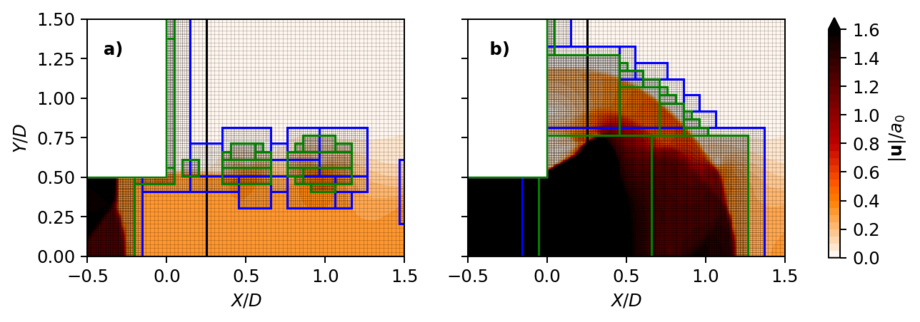
Figure 3 shows the contours of the dimensionless velocity together with the adaptive grid. The initial flow conditions are \(M_0=2.62\) and \(M_b=0.38\) for the shock Mach number and the background Mach number, respectively. The comparison of the two figures shows that the adaptive grid enables a high resolution of the high gradients and discontinuities. In both figures it can be clearly seen that only the areas of the grid around the embedded edges, the vortices formed by Kevin-Helmholtz instabilities in the shear layer of the background jet and those of the shock front have been refined. The other areas of the flow, on the other hand, are only mapped on the coarsest grid.
References
| [1] | M. J. Berger and J. Oliger. Adaptive mesh refinement for hyperbolic partial differential equations. Journal of Computational Physics, 53(3):484-512, 1984. |
| [2] | B. C. Bobusch, P. Berndt, C. O. Paschereit, and R. Klein. Shockless Explosion Combustion: An Innovative Way of Efficient Constant Volume Combustion in Gas Turbines. Combustion Science and Technology, 186(10-11):1680-1689, 2014. |
| [3] | N. Gokhale, N. Nikiforakis, and R. Klein. A dimensionally split Cartesian cut cell method for hyperbolic conservation laws. Journal of Computational Physics, 364:186-208, 2018. |
| [4] | B. S. Thethy, M. R. Haghdoost, B. S. Rhiannon Kirby, M. Nadolski, C. Zenker, M. Oevermann, R. Klein, K. Oberleithner, and D. Edgington-Mitchell. Diffraction of shock waves through a non-quiescent medium. Journal of Fluid Mechanics, 944:A39, 2022. |
| [5] | W. Zhang, A. Almgren, V. Beckner, and J. B. et al. AMReX: a framework for block-structured adaptive mesh refinement. Journal of Open Source Software, 4(37):1370, 2019. |
Virtual engine development VI

Aircraft engines must be sustainably improved in terms of emissions, efficiency and noise. This research project aims to combine the enormous potential of artificial intelligence and machine learning with the latest methods of optimisation and process integration in order to design the design assistance systems of the future using engine technology as an example.
External partners:
- Rolls-Royce Germany
- TU Berlin
- TH Brandenburg
- FRIENDSHIP SYSTEMS
Chairs involved at the BTU:
- Chair of Numerical Mathematics and Scientific Computing (Head)
- Chair of Structural Mechanics and Vehicle Vibrational Technology
- Chair of Aeroengine Design
- Chair of Applied Mathematics
Chair of Polymer-based Lightweight Design