Der Fokus der Forschungsaktivitäten am Fachbereich liegt in der Modellierung und Simulation strömungsmechanischer Probleme in Naturwissenschaft und Technik mittels CFD (Computational Fluid Dynamics). Im Detail handelt es sich um folgende Teilgebiete:
- Numerische Strömungsmechanik
- Mehrphasenströmungen (Sprays, Gas-Feststoff Strömungen)
- Turbulente Verbrennung (insbesondere motorische Verbrennung)
- Niederdimensionale, stochastische Modellierung für Verbrennungsprozesse und Mehrphasenströmungen
- Modellentwicklung für turbulente Verbrennungsprozesse
- Modellentwicklung für Mehrphasenströmungen
- High-Performance Computing
Im Folgenden finden Sie weiterführende Informationen zu unsereren aktuellen Forschungsaktivitäten.
Disperse Mehrphasensysteme
Disperse Mehrphasenströmungen sind dynamische Systeme zweier oder mehrerer Phasen, von denen mindestens eine in Form feiner Partikel in einem Fluid verstreut ist. In Natur und Technik sind solche Systeme allgegenwärtig. Das Wettergeschehen, Meeresströmungen und der Blutkreislauf sind nur wenige Beispiele für ihr zahlreiches Vorkommen in der Natur, während ihre Bedeutung in der Technik durch Beispiele wie Antriebssysteme, Energie- und Wärmetechnik und Fertigungstechnologien verdeutlicht wird. Die numerische Modellierung solcher Systeme ist besonders anspruchsvoll in Bezug auf die mathematische Darstellung der dispersen Phase und der damit verbundenen physikalischen Phänomene wie beispielsweise Turbulenz und verschiedene Mechanismen des Massen-, Impuls-, und Energieaustauschs.
Modellierungsansätze
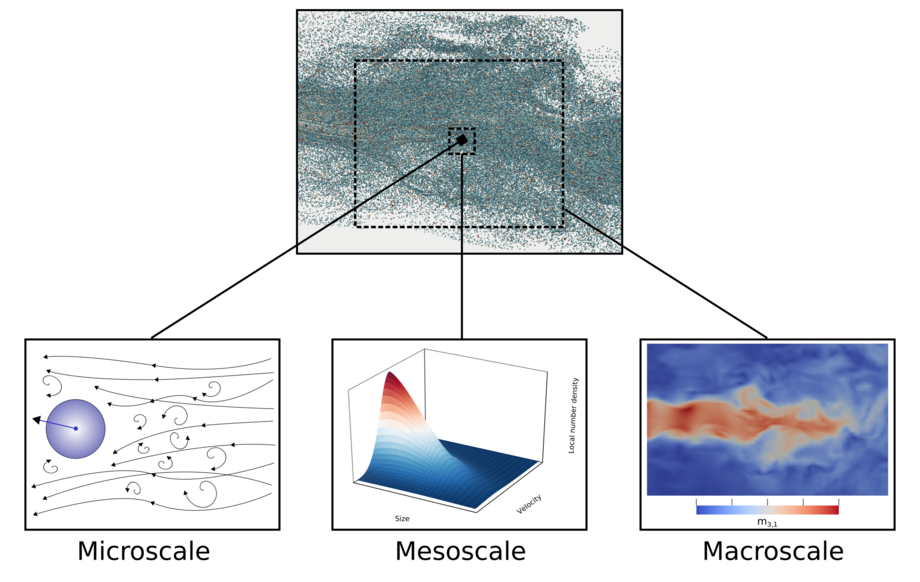
Mathematische Darstellungen des dispersen Subsystems können in mikroskopische, mesoskopische oder makroskopische Modellierungsansätze unterteilt werden:
- Mikroskopische Modelle erfassen physikalische Prozesse bis hin zur Partikelebene. Solche Ansätze sind zweifellos mit dem höchsten Detaillierungsgrad verbunden, erfordern allerdings Rechenkapazitäten, die möglicherweise für viele physikalische Anwendungen zu hoch sind.
- Mesoskopische Modelle zielen auf eine statistische Darstellung der lokalen Population ab. Diese ist in Form einer Anzahldichtefunktion (number density function, NDF) gegeben, deren Entwicklung durch eine sogenannte Populationsbilanzgleichung (population balance equation, PBE) beschrieben wird.
- Makroskopische Modelle sind oft vorteilhaft und effizienter, da die Zielgrößen numerischer Simulationen in vielen Fällen makroskopische Größen wie Konzentration, Masse, Impuls oder kinetische Energie sind.
Unsere Forschung konzentriert sich primär auf einen bestimmten makroskopischen Modellierungsansatz, die quadraturbasierten Momentenmethoden (quadrature-based moment methods, QBMM).
Quadraturbasierte Momentenmethoden
QBMM basieren auf der makroskopischen Beschreibung in Form von Momenten der NDF. Die Momentengleichungen können direkt aus der zugrundeliegenden PBE abgeleitet werden. Unter Berücksichtigung nur einer internen Koordinate \(\xi\) sowie Advektion und Diffusion mit der Driftfunktion \(\mathcal{A}(\xi)\) und Diffusivität \(\mathcal{D}(\xi)\) folgt die NDF \(n\) über die Zeit \(t\) der Gleichung
\(\frac{\partial n(\xi, t)}{\partial t} = - \frac{\partial }{\partial \xi} \left[ \mathcal{A}(\xi) \, n(\xi, t) \right] \; + \; \frac{\partial^2 }{\partial \xi^2} \left[ \mathcal{D}(\xi) \, n(\xi, t) \right]\).
Wendet man darauf die Definition des \(k\)-ten Moments \(m_k = \int_\Omega \xi^k n(\xi) \mathrm{d} \xi\) an, so ergibt sich für die \(k\)-te Momentengleichung
\(\frac{\mathrm{d} m_k(t)}{\mathrm{d} t} = - k \int_\Omega \xi^{k-1} \, \mathcal{A}(\xi) \, n(\xi, t) \mathrm{d} \xi \; + \; k(k-1) \int_\Omega \xi^{k-2} \, \mathcal{D}(\xi) \, n(\xi, t) \mathrm{d} \xi\).
Die Momentengleichungen sind also in dieser Form ohne Kenntnis der NDF nicht geschlossen lösbar. QBMM bieten eine Lösung dieses Schließungsproblems durch Anwendung von Quadraturformeln, d.h.
\(\frac{\mathrm{d} m_k(t)}{\mathrm{d} t} \approx - k \sum\limits_j w_j \, \xi_j^{k-1} \, \mathcal{A}(\xi_j) \; + \; k(k-1) \sum\limits_j w_j \, \xi_j^{k-2} \, \mathcal{D}(\xi_j)\).
Sind die Quadraturknoten \(\xi_j\) und Gewichte \(w_j\) die Knoten und Gewichte der Gauß-Quadratur mit der Gewichtsfunktion \(n\), so wird die Methode zur Schließung der Momentengleichungen als Quadraturmethode der Momente (quadrature method of moments, QMOM) [1] bezeichnet. Diese ist die Basis zahlreicher abgeleiteter Quadraturmethoden, siehe [2]. All diese Methoden haben gemeinsam, dass die gesuchte Quadraturformel ausschließlich aus der bekannten Information in Form von Momenten berechnet werden kann. Im Rahmen unserer Forschung haben wir eine Erweiterung der QMOM durch Anwendung der von Laurie [3] vorgestellten Anti-Gauß-Quadraturformeln entwickelt, die insbesondere die Qualität der Approximation bei stark nichtlinearen Problemen verbessern soll.
Ergebnisse: Tropfenzerfall
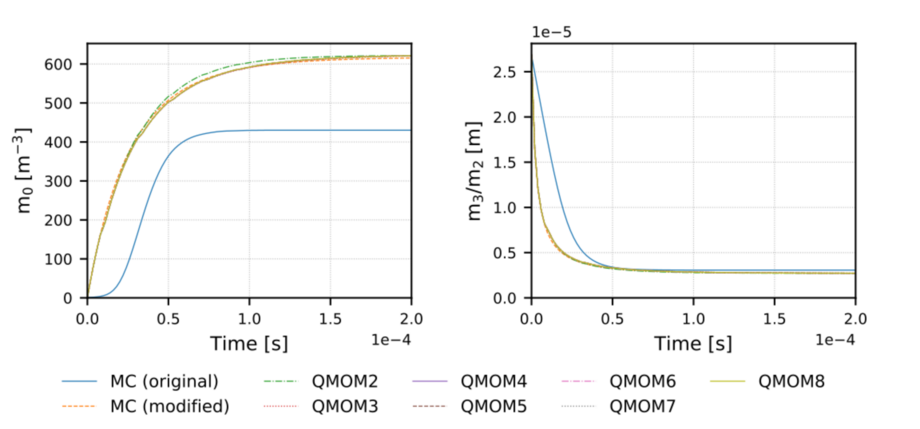
Im Rahmen unserer Forschungsaktivitäten haben wir die Momententransportgleichungen für eine modifizierte Version des weitverbreiteten Reitz-Diwakar-Modells für Tropfenzerfall [4] formuliert und zur Schließung die QMOM angewendet. Abb. 2 zeigt den Vergleich mit hochaufgelösten Monte-Carlo-Simulationen der PBE in Bezug auf die totale Tropfenanzahlkonzentration \(m_0\) sowie den mittleren Sauterdurchmesser \(m_3/m_2\) . Durch die Anwendung der QMOM mit mehr als zwei Quadraturknoten kann eine hohe Genauigkeit mit nur einem Bruchteil der Rechenkosten erreicht werden.
Ergebnisse: Turbulenzinduzierte Diffusion
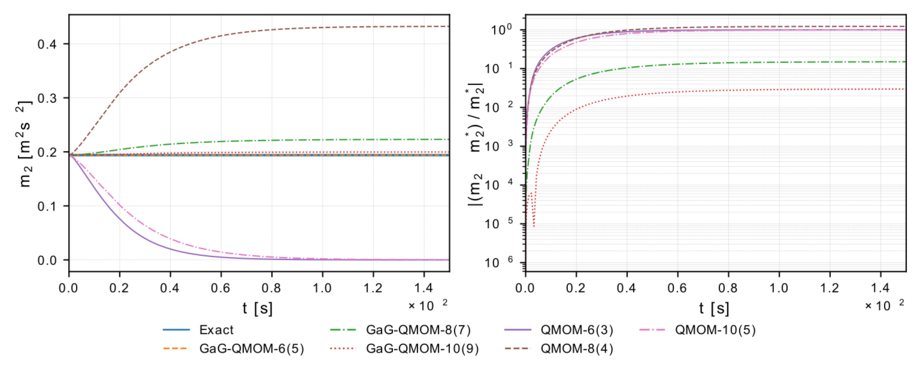
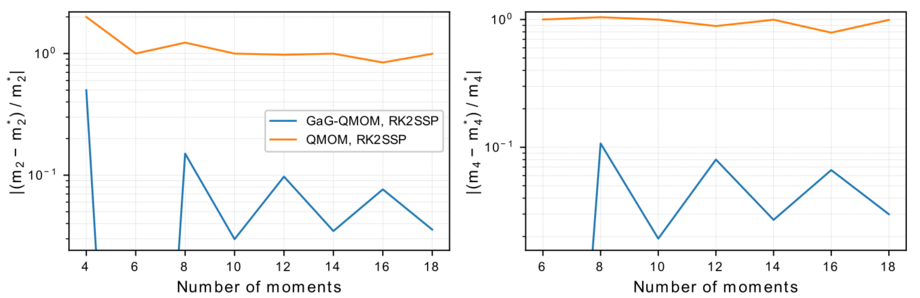
Unsere Erweiterung der QMOM, die Gauß/anti-Gauß QMOM (GaG-QMOM) haben wir auf ein räumlich homogenes turbulentes System angewandt. Die stark nicht-linearen turbulenzinduzierten Terme in der PBE stellen QBMM vor besondere Herausforderungen. Wie in Abb. 3 und Abb. 4 zu sehen, führt die Anwendung der GaG-QMOM in allen Fällen zu einer erheblichen Steigerung der Genauigkeit.
Literaturhinweise
| [1] | R. McGraw. Description of aerosol dynamics by the quadrature method of moments. Aerosol Sci. Tech., 27(2):255–265, 1997. |
| [2] | D. L. Marchisio and R. O. Fox. Computational Models for Polydisperse Particulate and Multiphase Systems. Cambridge University Press, 2013. |
| [3] | D. Laurie. Anti-Gaussian quadrature formulas. Math. Comput., 65(214):739–747, 1996. |
| [4] | R. D. Reitz and R. Diwakar. Effect of drop breakup on fuel sprays. SAE Tech. Pap., 860469,1986. |
Überblick und Ziel der Forschung
In Kooperation mit der Arbeitsgruppe Geophysical Fluid Dynamics der FU Berlin erforschen wir die theoretischen Rahmenbedingungen der Shockless Explosion Combustion (SEC), welches ein völlig neues Betriebskonzept für Gasturbinen darstellt. Wesentliche Grundlage einer SEC stellt dabei die kontrollierte homogene Selbstzündung des Treibstoffes dar, wodurch eine dynamische Annäherung an eine energetisch günstigere Gleichraumverbrennung (constant volume combustion, CVC) erreicht werden soll. [2] Die numerische Untersuchung der hier auftretenden Strömungen erfolgt auf sehr kleinen Zeit- und Längenskalen, was auch einen erheblichen Aufwand für den numerischen Strömungslöser (Computational Fluid Dynamics, CFD) erfordert. Daher entwickeln wir einen eigenen CFD-Löser und legen dabei besonderes Augenmerk auf effiziente numerische Methoden und Parallelisierung der Simulationen. Im Folgenden geben wir einen groben Überblick über die von uns verwendeten numerischen Methoden und konzentrieren uns insbesondere auf Methoden zur adaptiven Gitterverfeinerung (adaptive mesh refinement, AMR).
Numerische Methoden
Die allgemeine Grundlage für die numerische Lösung der hier behandelten Probleme sind die reaktiven Euler-Gleichungen für mehrere Spezies. Diese lauten in ihrer drei-dimensionalen konservativen Form:
\begin{gather}
\frac{\partial \mathbf{U}}{\partial t}
+ \frac{\partial \mathbf{F}(\mathbf{U})}{\partial x}
+ \frac{\partial \mathbf{G}(\mathbf{U})}{\partial y}
+ \frac{\partial \mathbf{H}(\mathbf{U})}{\partial z}
= \mathbf{S}(\mathbf{U}) \,, \label{eq:eulerEquation} \\
\mathbf{U} = \begin{bmatrix}
\rho \\ \rho u \\ \rho v \\ \rho w \\ \rho E \\ \rho Y_s
\end{bmatrix} ,\,
\mathbf{F} = \begin{bmatrix}
\rho u \\ \rho u^2+p \\ \rho uv \\ \rho uw \\ u(\rho E+p) \\ \rho u Y_s
\end{bmatrix} ,\,
\mathbf{G} = \begin{bmatrix}
\rho v \\ \rho uv \\ \rho v^2+p \\ \rho vw \\ v(\rho E+p) \\ \rho v Y_s
\end{bmatrix} ,\,
\mathbf{H} = \begin{bmatrix}
\rho w\\ \rho uw \\ \rho vw \\ \rho w^2+p \\ w(\rho E+p) \\ \rho w Y_s
\end{bmatrix} ,\, \label{eq:eulerComponents}
\end{gather}
wobei \(\rho\) die Dichte, \(\mathbf{u}=(u,v,w)\) die Geschwindigkeit, \(E=e+||\mathbf{u}||^2/2\) die Gesamtenergie, \(e\) die innere Energie, \(p\) der Druck und \(Y_s,\,s=1,\ldots,N_s-1\) die Massenanteile der reaktiven Spezies sind, die so normiert sind, dass sie sich zu Eins summieren. Die obigen Gleichungen werden durch die Approximation als kalorisch perfektes Gas \(p=\rho(\gamma-1)e\) geschlossen, wobei \(\gamma=c_p/c_v\) das Verhältnis der spezifischen Wärmen ist. Der Term \(\mathbf{S}(\mathbf{U})\) ist ein Platzhalter für jeden möglichen Quellterm, der z. B. äußere Kräfte, chemische Reaktionen oder jegliche Zufuhr von Masse, Impuls, Energie oder Spezies berücksichtigt. Zur Berechnung der numerischen Lösung der obigen Gleichungen verwenden wir vollständig konservative Finite-Volumen-Schemata, die auf blockstrukturierten kartesischen Gittern diskretisiert sind. Dank der Verwendung der externen C++-Bibliothek AMReX [5] in unserem CFD-Löser können wir das Gitter in den interessanten Regionen durch AMR-Techniken [1] lokal verfeinern. Um die Stabilität kleiner oder unregelmäßiger Zellen zu gewährleisten, die durch die Einbettung komplexer Geometrien in die strukturierten Gitter entstehen, verwenden wir eine konservative Cut-Cell-Methode [3].
Adaptive Gitterverfeinerung
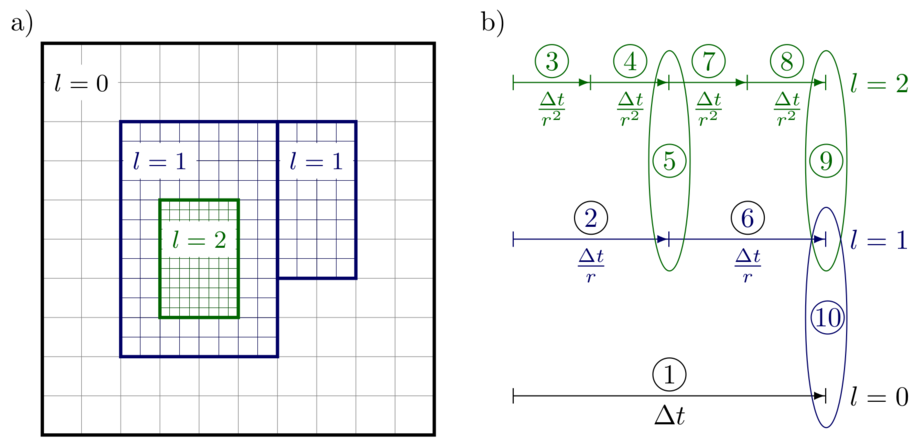
Abbildung 1 a) zeigt eine vereinfachte Skizze eines adaptiven kartesischen Gitters mit insgesamt drei Ebenen \((l=0,1,2)\), wobei das Rechengebiet auf jeder AMR-Ebene in eine Vielzahl von rechteckigen Gebieten zerlegt wird. Die fettgedruckten Linien stellen Gittergrenzen dar und alle Zellen jeder AMR-Ebene \(l_i\) werden mit einem Verfeinerungsverhältnis \(r\) im Vergleich zur Ebene \(l_{i-1}\) verfeinert. Für eine effiziente Zeitintegration auf adaptiven Gittern können wir den so genannten Subcycling-in-Time-Ansatz [5] verwenden, bei dem jede AMR-Ebene mit ihrer eigenen Zeitschrittweite \(\Delta t / r^l\) weiterentwickelt wird und eine Synchronisation stattfindet, wenn die Ebene \(l_i\) und \(l_{i-1}\) denselben Zeitpunkt erreicht haben. Dieser Ansatz ist in Abbildung 1 b) als Beispiel für drei Ebenen dargestellt. Bei diesem Ansatz treten zwei Probleme auf: (i) Die groben Daten der Ebene \(l_{i-1}\) sind nicht unbedingt gleich dem Durchschnitt der feineren Daten auf der Ebene \(l_i\). (ii) Aufgrund inkonsistenter Flüsse über die Grob-Fein-Grenzflächen wird die Erhaltung von Masse, Impuls oder Energie verletzt. Daher müssen wir in jedem Synchronisationsschritt (i) die Daten des Grobgitters mit gemittelten Daten des überlagernden Feingitters ersetzen und (ii) eine Flusskorrektur an den Grob-Fein-Grenzflächen vornehmen.
Ergebnisse
Hier präsentieren wir einige ausgewählte Ergebnisse von Simulationen zur Untersuchung der Beugung von Stoßwellen durch nicht ruhende Medien [4]. Für diese Simulationen betrachten wir ein eindimensionales Rohr, das von einem vorgegebenen Massenstrom durchströmt und in dem nach einer gewissen Zeit ein Stoß implementiert wird. An das Rohr schließt sich ein zweidimensionales Plenum an, in dem der Schock gebeugt wird. Hier beschränken wir die Simulationen auf zwei Dimensionen, keine Spezies und fügen einen zusätzlichen geometrischen Quellterm hinzu:
\begin{equation}
\mathbf{S}(\mathbf{U}) = - \frac{1}{y} \begin{bmatrix}
\rho v ,& \rho uv ,& \rho v^2 ,& v(\rho E+p)
\end{bmatrix}^\text{T},
\end{equation}
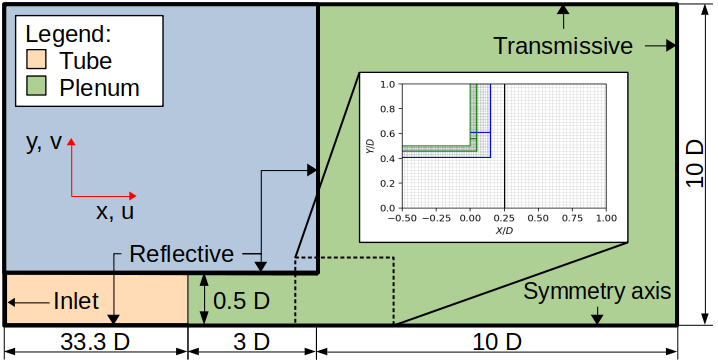
der die zylindrische Symmetrie um die \(x\)-Achse berücksichtigt. Eine Skizze unseres Simulationsgebiets mit Randbedingungen (boundary conditions, BC's) ist in Abbildung 2 dargestellt, wobei die eingeschobene Abbildung Details des eingebetteten Plenums in dem strukturierten adaptiven Gitter mit insgesamt drei Ebenen zeigt.
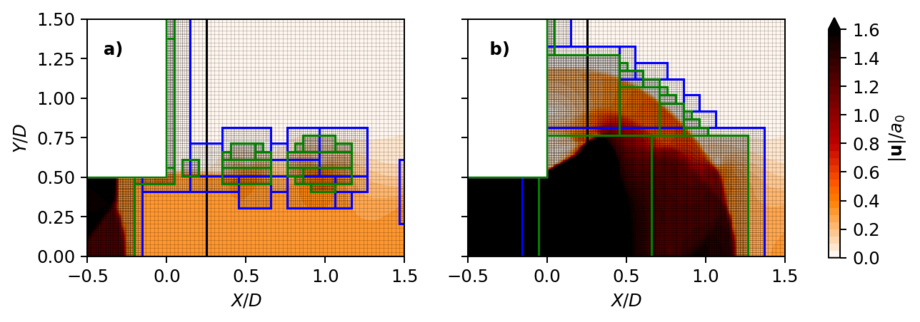
Abbildung 3 zeigt die Konturen der dimensionslosen Geschwindigkeit zusammen mit dem adaptiven Gitter. Die anfänglichen Strömungsbedingungen sind \(M_0=2.62\) und \(M_b=0.38\) für die Schock-Machzahl bzw. die Hintergrund-Machzahl. Der Vergleich der beiden Abbildungen zeigt, dass das adaptive Gitter eine hohe Auflösung der hohen Gradienten und Diskontinuitäten ermöglicht. In beiden Abbildungen ist deutlich zu erkennen, dass nur die Bereiche des Gitters um die eingebetteten Ränder, die durch Kevin-Helmholtz-Instabilitäten gebildeten Wirbel in der Scherschicht des Hintergrundstrahls und die der Schockfront verfeinert wurden. Die anderen Bereiche der Strömung hingegen sind nur auf dem gröbsten Gitter abgebildet.
Literaturhinweise
| [1] | M. J. Berger and J. Oliger. Adaptive mesh refinement for hyperbolic partial differential equations. Journal of Computational Physics, 53(3):484-512, 1984. |
| [2] | B. C. Bobusch, P. Berndt, C. O. Paschereit, and R. Klein. Shockless Explosion Combustion: An Innovative Way of Efficient Constant Volume Combustion in Gas Turbines. Combustion Science and Technology, 186(10-11):1680–1689, 2014. |
| [3] | N. Gokhale, N. Nikiforakis, and R. Klein. A dimensionally split Cartesian cut cell method for hyperbolic conservation laws. Journal of Computational Physics, 364:186–208, 2018. |
| [4] | B. S. Thethy, M. R. Haghdoost, B. S. Rhiannon Kirby, M. Nadolski, C. Zenker, M. Oevermann, R. Klein, K. Oberleithner, and D. Edgington-Mitchell. Diffraction of shock waves through a non-quiescent medium. Journal of Fluid Mechanics, 944:A39, 2022. |
| [5] | W. Zhang, A. Almgren, V. Beckner, and J. B. et al. AMReX: a framework for block-structured adaptive mesh refinement. Journal of Open Source Software, 4(37):1370, 2019. |

Virtuelle Triebwerksentwicklung VI
Flugtriebwerke müssen in Hinblick auf Emissionen, Effizienz und Lärm nachhaltig verbessert werden. Im Rahmen dieses Forschungs- vorhabens soll das enorme Potential der künstlichen Intelligenz und des maschinellen Lernens mit modernsten Methoden der Optimierung und Prozessintegration verknüpft werden, um Entwurfsassistenzsysteme der Zukunft am Beispiel der Triebwerkstechnik zu konzipieren.
externe Partner:
- Rolls-Royce Deutschland
- TU Berlin
- TH Brandenburg
- FRIENDSHIP SYSTEMS

beteiligte Fachgebiete an der BTU:
- FG Numerische Mathematik und Wissenschaftliches Rechnen (Leitung)
- FG Strukturmechechanik und Fahrzeugschwingungen
- FG Flug-Triebwerksdesign
- FG Angewandte Mathematik
FG Polymerbasierter Leichtbau