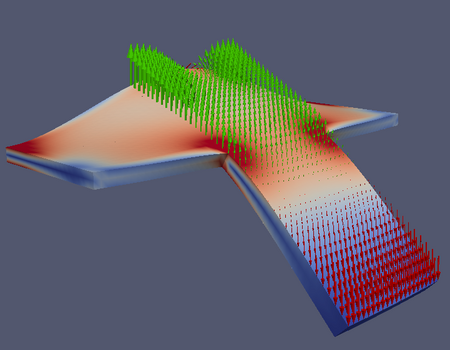
In Optimal Control applications, it is often desirable for the control system to only act on a part of the entire domain. This means that actuators do not have to be placed everywhere and costs can be saved. By using non-smooth terms in the objective functional, controls can be found that are sparse, i.e. that disappear over a large part of the control domain. Here, the points at which the control becomes active are not predetermined. It is also possible to use special objective functionals to obtain structured optimal controls, e.g. with a strip or ring structure. The video on the right shows a time-dependent application with a parabolic differential equation. The position of the control does not depend on time and its placement is determined by the optimisation.

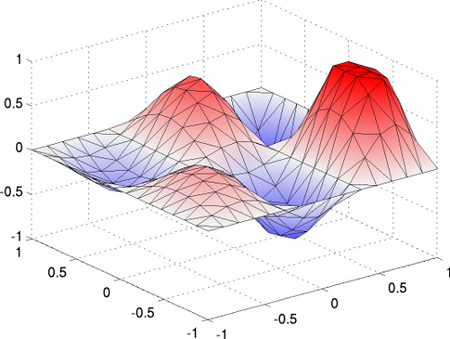
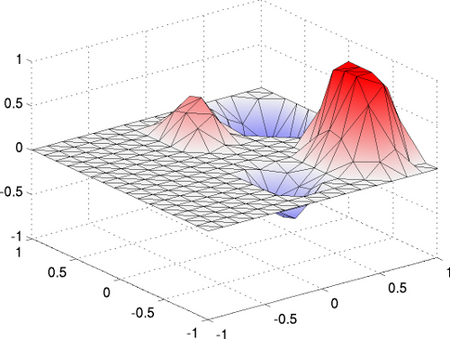
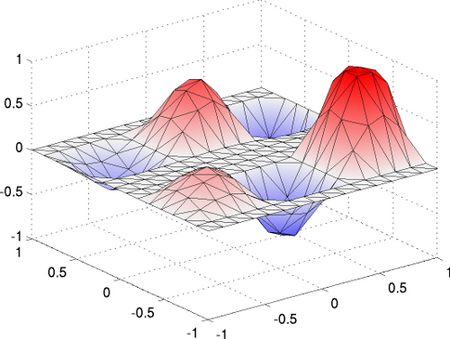
Mathematical programs with complementarity constraints (MPCCs) represent a class of non-linear optimisation problems that present particular difficulties due to their constraints. Thus, classical constraint qualifications (such as the Mangasarian-Fromovitz-CQ) are violated and one has to rely on adapted optimality systems and solution methods. I am interested in generalisations of finite-dimensional theory, in particular in the infinite-dimensional case. A typical example is the optimal control of the obstacle problem. There are further applications, for example in plasticity, where the switching between elastic and plastic material behaviour can be described by a complementarity condition. The pictures on the right show the optimal control of quasi-static plasticity with springback, there is also a video.

Many interesting applications, such as Newton's problem of least resistance or the monopolist problem from Economic Sciences, lead to variational problems in which the function being sought is convex. Due to this convexity condition, classical solution techniques are not applicable. My key research area is the development of new numerical methods to solve such problems efficiently. Solutions to Newton's problem of least resistance for different heights are shown on the right. More information can be found in the article The Numerical Solution of Newton's Problem of Least Resistance.