Schwerpunkte
Optimale Steuerung von partiellen Differentialgleichungen mit sparsen Kontrollen
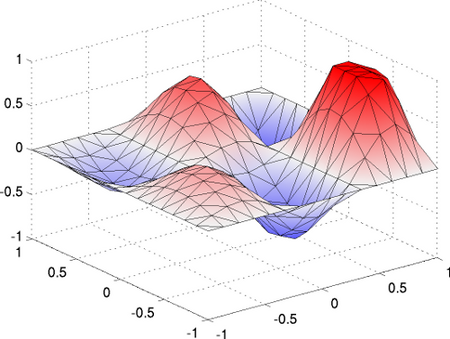
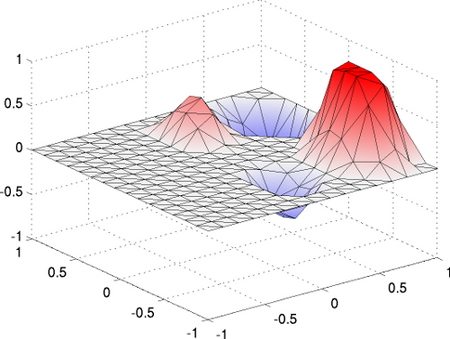
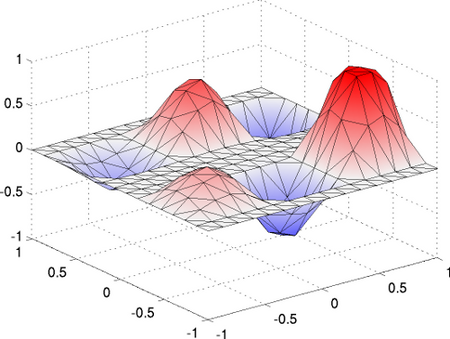
In Anwendungen der optimalen Steuerung ist es oft wünschenswert, dass die Steuerung nur auf einem Teil des ganzen Gebietes wirkt. Dadurch müssen Aktuatoren nicht überall plaziert werden und es können Kosten gespart werden. Durch den Einsatz von nichtglatten Termen im Zielfunktional können Steuerungen gefunden werden, die sparse sind, also die auf einem großen Teil des Kontrollgebietes verschwinden. Die Stellen, an denen die Steuerung aktiv wird, sind dabei nicht vorgegeben. Weiter ist es auch möglich, durch spezielle Zielfunktionale strukturierte optimale Steuerungen zu erhalten, z.B. mit streifenweiser oder ringförmiger Struktur. Das Video rechts zeigt eine zeitabhängige Anwendung bei einer parabolischen Differentialgleichung. Die Position der Steuerung hängt nicht von der Zeit ab und die Lage wird durch die Optimierung bestimmt.
Optimierungsprobleme mit Komplementaritätsnebenbedingungen
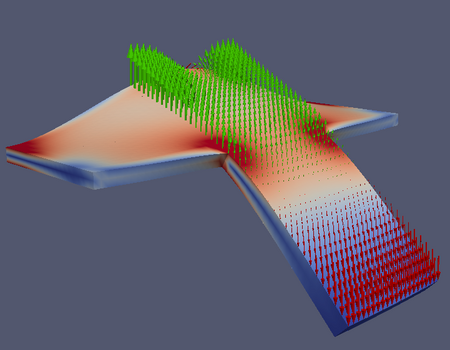
Optimierungsprobleme mit Komplementaritätsnebenbedingungen (mathematical programs with complementarity constraints, MPCCs) stellen eine Klasse von nichtlinearen Optimierungsaufgaben dar, die durch ihre Nebenbedingungen besondere Schwierigkeiten aufweisen. So sind klassische Constraint Qualifications (wie die Mangasarian-Fromovitz-CQ) verletzt und man ist auf angepasste Optimalitätssysteme und Lösungsverfahren angewiesen. Dabei liegt mein Interesse auf Verallgemeinerungen der endlichdimensionalen Theorie, insbesondere auf dem unendlichdimensionalen Fall. Ein typisches Beispiel dafür ist die Optimale Steuerung des Hindernisproblems (obstacle problem). Weitere Anwendungen gibt es zum Beispiel in der Plastizität, bei der das Umschalten zwischen elastischen und plastischen Materialverhalten durch eine Komplementaritätsbedingung beschrieben werden kann. Die Bilder auf der rechten Seite zeigen die optimale Steuerung von quasistatischer Plastizität mit Rückfederung, dazu gibt es auch ein Video.
Optimierung mit Konvexitätsbeschränkungen
Viele interessante Anwendungen, wie Newtons Problem des geringsten Widerstandes oder das Monopolistenproblem aus den Wirtschaftswissenschaften, führen auf Variationsprobleme, bei denen die gesuchte Funktion konvex ist. Durch diese Konvexitätsbedingung sind klassische Lösungstechniken nicht anwendbar. Mein Forschungsschwerpunkt liegt dabei auf der Entwicklung neuer numerischer Verfahren, um solche Probleme effizient zu lösen. Lösungen für Newtons Problem des geringsten Widerstandes für verschiedene Höhen sind auf der rechten Seite zu sehen. Mehr Informationen gibt es im Artikel The Numerical Solution of Newton's Problem of Least Resistance.