BTU overview
Faculty 3
Chair of Control Systems and Network Control Technology Prof. Dr.-Ing. Johannes Schiffer

Control Design and Analysis of Nonlinear Systems

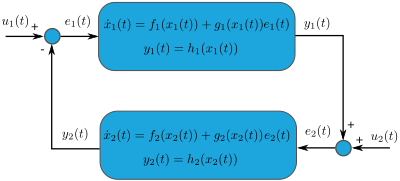
Many phenomena in engineering applications exhibit inherently nonlinear characteristics. This applies to diverse domains, such as mechanism, transportation, power and biological systems. Our research activities in this area are geared towards providing system analysis and controller synthesis methods that enable the development of new applications for real-world systems. To this end, we seek to explicitly account for the nonlinear system properties at hand, instead of trying to dominate its nonlinearities. This can be achieved by using ideas from energy-based modeling and control as well as Lyapunov-based stability theory for dynamical systems with several disjoint invariant sets.

Current topics of interest include:

  • Global stability properties and control design for state periodic systems
  • Input-to-state-stability (ISS)
  • Passivity-based control
  • Delay-robustness of networked systems

People

Cooperations

Funding

Selected publications

J.Schiffer, D.Efimov, and R. Ortega, “Global Synchronization Analysis of Droop-Controlled Microgrids - A Multivariable Cell Structure Approach”, Automatica, 109, Art. no. 108550, 2019
doi

D. Efimov and J. Schiffer, “On Boundedness of Solutions of State Periodic Systems: A Multivariable Cell Structure Approach”, IEEE Transactions on Automatic Control, 64 (10), pp. 4094-4104, 2019
doi

D. Efimov, J. Schiffer, N. Barabanov, and R. Ortega, “A Relaxed Characterization of ISS for Periodic Systems with Multiple Invariant Sets”, European Journal of Control, 37, pp. 1-7, 2017
doi

N. Barabanov, J. Schiffer, R. Ortega, and D. Efimov, “Conditions for Almost Global Attractivity of a Synchronous Generator Connected to an Infinite Bus”, IEEE Transactions on Automatic Control,62 (10), pp. 4905-4916, 2017
doi

J. Schiffer, E. Fridman, R. Ortega, and J. Raisch, “Stability of a Class of Delayed Port-Hamiltonian Systems with Application to Microgrids with Distributed Rotational and Electronic Generation”, 
Automatica, 74 (12), pp. 71-79, 2016
doi