Das Mengenüberdeckungsproblem

Dies ist ein klassisches Problem der kombinatorischen Optimierung mit unzähligen Anwendungen. Im Lehrstuhl Ingenieursmathematik und Numerik der Optimierung wird an solchen Problemen geforscht.

Im Escaperoom wird man Mengenüberdeckungsprobleme lösen müssen.

Das Partitionsproblem

Dies ist ein kombinatorisches Problem als auch ein Optimierungsproblem. Am Lehrstuhl Ingenieursmathematik und Numerik der Optimierung werden Partitionierungsprobleme unter anderem bei der Einsatzplanung von Flugdrohnen genutzt.

Im Escaperoom wird man ein Partitionsproblem lösen müssen.

Lineare Gleichungssysteme

Lineare Gleichungssysteme sind ein grundlegender Bestandteil zahlreicher naturwissenschaftlicher Erkenntnisse - sämtliche numerische Simulationen basieren auf solchen Rechnungen. Im Fachgebiet Optimale Steuerung von Prof. Wachsmuth werden lineare Gleichungssysteme zur Näherung und Lösung von Differentialgleichungen (z.B. bei der Optimierung von physikalischen Prozessen) angewandt.

Im Escaperoom ist ein solches lineares Gleichungssystem zu lösen.

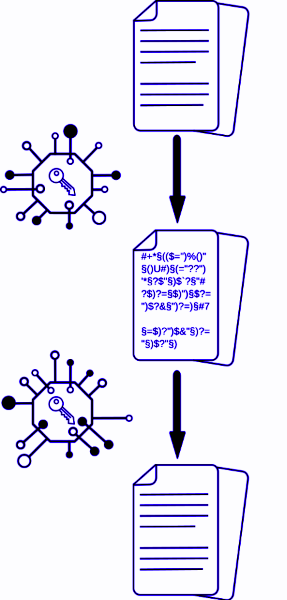
Kryptographie

In der Kryptographie beschäftigt man sich mit der Ver- und Entschlüsselung von Daten, um eine sichere Kommunikation zwischen zwei oder mehreren Akteuren zu ermöglichen. An der BTU beschäftigt man sich im Rahmen des Masterstudiengangs Cyber Security genauer mit kryptographischen Erkenntnissen.

Im Escaperoom werdet ihr ein Kryptographieproblem lösen.

Kürzeste-Wege-Probleme

Dies sind klassische Probleme der Netzwerkoptimierung und Graphentheorie. Seit den 1950er Jahren sind Algorithmische Lösungsverfahren bekannt.  Der Lehrstuhl Diskrete Mathematik und Grundlagen der Informatik forscht z.B. an energieoptimalen Routen für Hybrid- und Elektrofahrzeuge sowie an der Frage, wie man Fahrradfahrer so durch die Stadt lotst, dass sie möglichst selten an roten Ampeln stehen müssen.

Im Escaperoom muss ein solcher kürzester Weg gefunden werden.