Vortragsangebote für Schulen
Die Professoren des Fachbereiches Mathematik bieten die folgenden, schülergerechten Vorträge an, in denen Themen der Mathematik exemplarisch präsentiert werden. Anfragen und Terminabsprachen bitte über Prof. Breuß.
Alles Zufall oder was?
"Alles Zufall oder was?" heißt das Thema, bei dem gezeigt wird, dass es eben nicht bloss Zufall ist, wer bei Glücksspielen gewinnt. Hinter dem vermeintlichen Chaos des Zufalls stehen Gesetzmäßigkeiten, deren Kenntnis und Anwendung durchaus Vorteile für die Spieler haben können. So kann zum Beispiel bei dem Spiel "Memory" außer einem guten Gedächtnis manchmal auch eine gewisse Strategie dem Glück etwas nachhelfen. Und bevor man sich in eine Spielhalle wagt, sollte man sich die Gewinnchancen beim Roulette erst einmal im "Trockenversuch" an der Tafel vorrechnen lassen. Schließlich erfahren die Zuhörer noch, dass man beim Lottospielen zwar nicht seine Gewinnchancen erhöhen kann, wohl aber die Gewinnerwartung."
Wie bohrt man viereckige Löcher aus?
Im Vortrag geht es um die mathematische Beschreibung und Lösung von Optimierungsaufgaben in der Geomerie. Insbesondere spielen solche geometrische Figuren eine Rolle, die sich allseitig berührend in einem gleichseitigen n- Eck drehen lassen. Diese heissen Reuleaux-Figuren. Sie spielen nicht nur beim Ausbohren eckiger Löcher, sondern auch bei vielen technischen Problemen eine wichtige Rolle. Einige dieser Anwendungen werden im Vortrag vorgestellt.
Zu schlau für den Stau -- Diskrete Optimierung im Verkehr
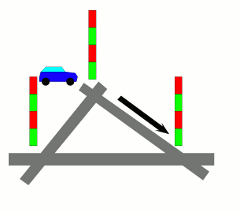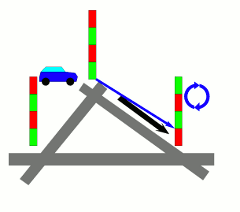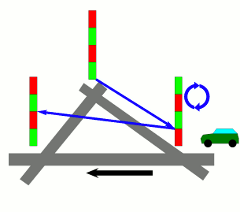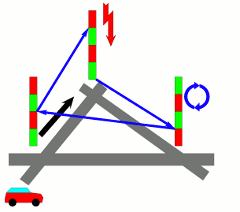
Wann haben Sie das letzte Mal vor einer roten Ampel gestanden und sich geärgert, dass nicht endlich mal jemand diese Ampeln richtig schaltet? Was heißt es eigentlich eine Ampel richtig zu schalten? Wie kann man Verkehr optimal durch ein Verkehrsnetz leiten? Und was hat das alles mit Mathematik zu tun? In dieser Vorlesung wollen wir uns mit einigen mathematischen Modellen und Ideen für die Optimierung von Verkehrsnetzen beschäftigen. Dabei sollen insbesondere Methoden aus dem Gebiet der Diskreten Optimierung und der Graphentheorie eine Rolle spielen. So werden wir untersuchen, wie man einen einzelnen kürzesten Weg in einem Netzwerk finden kann, aber auch wie man für viele Verkehrsteilnehmer gleichzeitig eine möglichst gute Routenführung ermitteln kann. Und wenn die Zeit reicht, werden wir auch noch ein paar Ideen vorstellen, wie man denn eine Ampel tatsächlich richtig schalten kann.
Kryptographie und große Primzahlen - wie sicher ist online-banking?
Aktuell diskutiert - die Frage nach der Sicherheit im Datenverkehr. Davon ist jeder persönlich betroffen, der sich im Internet bewegt. Die Mathematik 'großer' Primzahlen ist Grundlage der 'public-key' Verschlüsselung - eine grundlegende Methode der modernen Kryptographie. Wie groß müssen solche Primzahlen sein, wie findet man diese, wie funktioniert die Verschlüsselung?
Klassische Probleme und Paradoxa in der Wahrscheinlichkeitsrechnung
Der Vortrag widmet sich elementaren Begriffen aus der Stochastik und zeigt, dass in der Vergangenheit auch anerkannte Fachleute auf dem Gebiet der Mathematik wie z.B. Leibniz und d’Alembert mit der Lösung relativ einfacher Aufgaben ihre Probleme hatten und Irrtümern aufgesessen waren. So werden die seltsame Logik der Münzen und Würfel, ein populärer Trugschluss zum Gesetz der großen Zahlen und "unerwartete" Erwartungswerte unter die Lupe genommen. Weiterhin wird eine unkonventionelle Methode zur "Berechnung" der Kreiszahl pi mit der Buffonschen Nadelwurfmethode vorgestellt und die Funktionsweise eines Galton-Brettes erläutert.
Elementare komplexe Funktionen auf ihren Riemannschen Flächen
Nachdem die reellen Zahlen R als Äquivalenzklassen mit Ideen von D.Hilbert konstruiert worden sind, betrachten wir die Gaußsche Ebene der komplexen Zahlen C. Im Körper C zerfällt jedes Polynom n-ten Grades in Linearfaktoren nach dem Fundamentalsatz der Algebra. Wollen wir die n-te Potenzfunktion zn als umkehrbare Abbildung studieren, so werden wir auf die n-fache Überlagerungsfläche der punktierten komplexen Ebene C\{0} geführt. Deren Umkehrfunktion als n-te Wurzel z(1/n) ist dann eindeutig erklärt. Betrachten wir nun die komplexe Exponentialfunktion exp z über ihre Potenzreihe, so benötigt man die universelle Überlagerungsfläche von C\{0}, um diese Funktion umzukehren. Deren inverse Abbildung stellt die universelle komplexe Logarithmusfunktion log z auf ihrer Riemannschen Fläche dar, welche für geometrische Anwendungen eine zentrale Bedeutung besitzt. Diese Konstruktion wird explizit sowie elementar durchgeführt und durch eine Wendeltreppe veranschaulicht, deren Projektion auf die Ebene mehrdeutig ist. In unserem Grundkurs [S] zur Analysis haben wir das Komplexe zentral einbezogen, da sich erst so die Analysis in ihrer ganzen Schönheit entfalten kann. Weiter möchten wir an dieser Stelle das inspirierende Lehrbuch [S] von S. Hildebrandt zur Analysis als auch das interessante Werk [So] von T. Sonar zur Geschichte der Analysis empfehlen.
Literatur:
- [H] Hildebrandt, Stefan: Analysis 1 und 2. Springer-Lehrbuch, Springer-Verlag Berlin, Heidelberg 2001, 2002.
- [S] Sauvigny, Friedrich: Analysis - Grundlagen, Differentiation, Integrationstheorie, Differentialgleichungen, Variationsmethoden. Springer-Lehrbuch, Verlag Springer-Spektrum Berlin, Heidelberg, 2014.
- [So] Sonar, Thomas: 3000 Jahre Analysis. Springer-Verlag Berlin, Heidelberg, 2011.
Kann mein Laptop mir bei den (un-)geliebten Matheaufgaben helfen?
In diesem Vortrag wird anschaulich erklärt, wie bestimmte Integrale mit dem Laptop berechnet werden können. Dies ist von großer Bedeutung, da eine Reihe von Integralen nicht analytisch lösbar sind. Wir demonstrieren die vorgestellten Methoden anhand grafischer Darstellungen und Animationen.
Mathematik für digitale Bilder
Viele Menschen gehen heute mittels des Internets oder Handykameras alltäglich mit digitalen Bildern um. Dabei bieten digitale Bilder oft wesentlich mehr Inhalt als man üblicherweise etwa durch Produkte wie Photoshop darin erkennt. Im Vortrag wird gezeigt, wie man mit Mathematik tiefer gehende Informationen aus Bildern gewinnen kann. Schon relativ einfache Aufgabenstellungen führen dabei auf aktuelle Forschungsthemen.
