Rätsel
Aufgelistet sind alle mathematischen Hintergründe der gestellten Rätsel; diese spielen unter anderem in verschiedenen Forschungsgebieten eine wichtige Rolle.
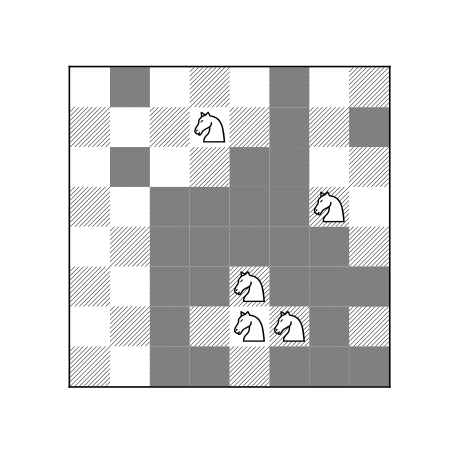
Das Mengenüberdeckungsproblem
Wo müssen Antennen gebaut werden, um effizient jeden Winkel einer Stadt mit Mobilfunk zu versorgen? Wo parkt man Rettungswagen, damit jeder Notfall im Landkreis in 15 Minuten medizinisch versorgt werden kann? Diese Fragen führen zum Mengenüberdeckungsproblem: Hierbei soll eine Grundmenge mit einer vordefinierten Auswahl an Teilmengen überdeckt werden. Jeder Teilmenge ist dabei ein Wert zugewiesen, und die Summe der Werte soll so gering wie möglich sein. Dies ist ein klassisches Problem der kombinatorischen Optimierung mit unzähligen Anwendungen. Im Lehrstuhl Ingenieursmathematik und Numerik der Optimierung wird an solchen Problemen geforscht.
Im Escaperoom hat man Mengenüberdeckungsprobleme bei dem Bienenwaben- sowie dem Schachrätsel lösen müssen.
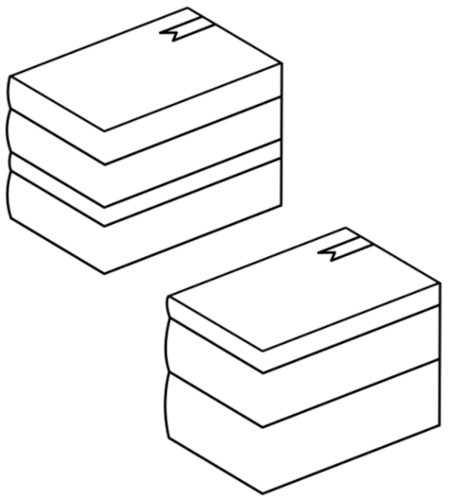
Das Partitionsproblem
Ein Paar will in den Urlaub fliegen, hat zwei Koffer und jede Menge Sachen zum Einpacken. Damit kein Koffer überladen wird, muss ein Partitionsproblem gelöst werden. Dies ist ein weiteres kombinatorisches Problem. Möchte man zudem die Differenz der beiden Gewichte so gering wie möglich halten,wird daraus ein Optimierungsproblem. Am Lehrstuhl Ingenieursmathematik und Numerik der Optimierung werden Partitionierungsprobleme unter anderem bei der Einsatzplanung von Flugdrohnen genutzt.
Das stapeln der regenbogenfarbigen Bücher ist ein solches Partitionsproblem.

Lineare Gleichungssysteme
Lineare Gleichungssysteme sind ein grundlegender Bestandteil zahlreicher naturwissenschaftlicher Erkenntnisse - sämtliche numerische Simulationen basieren auf solchen Rechnungen. Außerdem werden diese in Straßennetzproblemen, Ausgleichsrechnungen oder grafischen Darstellungen auf Computerbildschirmen eingesetzt. Ziel ist es, aus linearen Beziehungen die Werte der Variablen zu bestimmen. Im Fachgebiet Optimale Steuerung von Prof. Wachsmuth werden lineare Gleichungssysteme zur Näherung und Lösung von Differentialgleichungen (z.B. bei der Optimierung von physikalischen Prozessen) angewandt. Dabei treten Systeme mit Millionen von Unbekannten auf.
Das Mobilé ist eine Darstellung eines linearen Gleichungssystems.
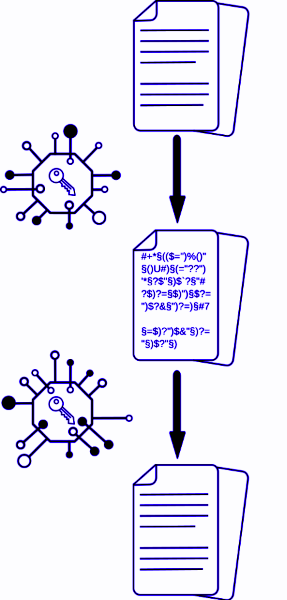
Kryptographie
In der Kryptographie beschäftigt man sich mit der Ver- und Entschlüsselung von Daten, um eine sichere Kommunikation zwischen zwei oder mehreren Akteuren zu ermöglichen. Es werden dabei Informationen mit Algorithmen in eine Form umgewandelt, die nur durch den Besitz eines geheimen Schlüssels wieder lesbar gemacht werden kann. Die Kryptographie spielt eine wesentliche Rolle im Bereich der sicheren Internetkommunikation. An der BTU beschäftigt man sich im Rahmen des Masterstudiengangs Cyber Security genauer mit kryptographischen Erkenntnissen.
Im Escaperoom wurden drei Bilder mithilfe von grafischer Kryptographie verschlüsselt.
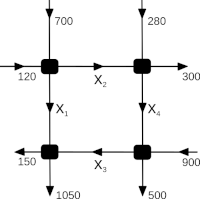
Kürzeste-Wege-Probleme
Wie findet das Navi den kürzesten Weg zwischen zwei Orten? Wie verlegt man kostengünstig das Glasfasernetz in einer ganzen Ortschaft? Diese Fragen sind klassische Probleme der Netzwerkoptimierung und Graphentheorie. Seit den 1950er Jahren sind Algorithmische Lösungsverfahren bekannt. Für aktuelle Fragestellungen müssen sie jedoch auch heute noch weiterentwickelt und angepasst werden. Der Lehrstuhl Diskrete Mathematik und Grundlagen der Informatik forscht z.B. an energieoptimalen Routen für Hybrid- und Elektrofahrzeuge sowie an der Frage, wie man Fahrradfahrer so durch die Stadt lotst, dass sie möglichst selten an roten Ampeln stehen müssen.
Das Richtungsschloss vor dem Stromschalter musste durch einen kürzesten Weg geöffnet werden.
