Thermodynamische Berechnungen
Nutzen und Aufwand thermodynamischer Berechnungen
Thermodynamische Berechnungen stellen ein wertvolles Werkzeug für das Studium komplexer chemischer Reaktionssysteme dar, aus denen eine Vielzahl von Informationen hervorgehen, die mit anderen Methoden nicht zugänglich sind, so z.B. Aussagen, ob Reaktionen thermodynamisch erlaubt sind oder nicht, ob eine Gleichgewichtsreaktion oder eine praktisch irreversible Reaktion vorliegt, ob thermodynamisch bedingte Reaktionstemperaturen existieren, ebenso wie quantitative Aussagen zum Einfluss von Reaktionsparametern auf die Lage von Gleichgewichten und über die unter Gleichgewichtsbedingungen auftretenden thermodynamisch stabilsten Reaktionsprodukte und deren Mengen.
Von besonderem Interesse ist die Beschreibung kinetischer Einflüsse auf den Reaktionsverlauf. Im Vergleich mit experimentellen Ergebnissen können unter kinetischer Kontrolle entstandene Reaktionsprodukte erkannt und zwischen thermodynamisch und kinetisch bedingten Reaktionstemperaturen unterschieden werden. Ebenso kann die Effizienz von Katalysatoren am Grad der Annäherung an den thermodynamisch möglichen Umsatz oder eines kinetisch bedingten höheren Umsatzes als den thermodynamisch möglichen beurteilt werden.
Thermodynamische Berechnungen können überdies zur Modellierung kinetisch bestimmter Reaktionssysteme eingesetzt werden. Hierzu wird die berechnete Bildung des jeweils thermodynamisch stabilsten Produktes bzw. einer in der Berechnung, jedoch im Experiment nicht auftretende Komponente in aufeinanderfolgenden Berechnungsroutinen unterdrückt. Daraus ergeben sich Stabilitätsreihen für die jeweiligen Reaktionsprodukte.
Die Erstellung eines thermodynamischen Datensatzes
Voraussetzung für eine erfolgreiche Berechnung ist ein Datensatz, der die freien Enthalpiefunktionen der im Reaktionssystem auftretender Stoffe und Phasen enthält. Die wesentlichste Herausforderung besteht in der Auswahl und in der Aufarbeitung der Daten, die zu einer thermochemisch richtigen Beschreibung des Stoffsystems führen sollen. Häufig tritt der Fall ein, dass gesuchte thermodynamische Größen entweder nicht vorliegen oder eine Fülle von Daten für einige wenige thermodynamische Größen (z.B. Standardbildungsenthalpien) existierten, die eine sehr starke Streuung aufweisen und einander teilweise widersprechen.
Für die Datenauswahl empfiehlt sich zunächst eine kritische Prüfung, inwieweit die vorliegenden Daten dem gesuchten Sachverhalt wirklich entsprechen (z.B. Fehlerangaben, die Reinheit der untersuchten Substanzen, unvollständige Stoffumsätze und mögliche Nebenreaktionen in reaktionskalorimetrischen Untersuchungen sowie Annahmen, Näherungen und Abschätzungen bei der Berechnung thermodynamischer Größen aus Messwerten) und ob aus den Beschreibungen der angewandten Messverfahren und den vorliegenden Messbedingungen Hinweise auf die Richtigkeit der Daten ableitbar sind. Liegen Datensätze mit vertauenswürdigen Daten vor, sind diese auf ihre Konsistenz zu prüfen. Hierzu zählt die Ermittlung von "Bestwerten", d.h. die Durchführung einer Optimierungsprozedur zur Bestimmung des Anpassungsgrades der einzelnen Datensätze an ein bereits bestehendes thermochemisches Modell oder die Erstellung eines eigenständigen thermochemischen Modells unter Variation der zur Verfügung stehenden Datensätze. Fehlen thermodynamische Größen, können diese durch Optimierungsroutinen aus anderen bekannten Datensätzen berechnet werden. Hierzu kommt das CALPHAD-Verfahren (calculation of phase diagrams) rekursiv zum Einsatz: Die richtige Wiedergabe des Phasendiagramms ist ein Kriterium für die Güte der optimierten Daten, womit die aus einem solchen Datensatz zurückgerechneten Größen eine hohe Wahrscheinlichkeit für ihre Richtigkeit besitzen. In jedem Fall müssen die erstellten Datensätze anhand der Berechnung solcher Reaktionen bzw. Prozesse auf Richtigkeit überprüft werden, die nicht als Eingangsdaten der Optimierung verwendet wurden.
Das Prinzip der Optimierung thermodynamischer Parameter
Die Optimierung thermodynamischer Daten verfolgt zwei grundlegende Ziele:
(1) Die Ermittlung optimierter thermodynamischer Parameter (d.h. die Parameter thermodynamischer Modelle) aus einer Vielzahl von Messungen, die unterschiedlichen Quellen entstammen oder sehr stark untereinander streuen. Dies ist gleichbedeutend mit der Gewinnung von "Bestwerten" aus den streuenden Messwerten.
(2) Die Berechnung fehlender thermodynamischer Daten, die experimentell nicht bestimmt wurden oder deren Bestimmung experimentell schwierig ist. Hierzu wird ein thermodynamisches Modell aus einer Vielzahl von Daten unterschiedlicher Herkunft erstellt, was der Erzeugung eines überbestimmten Systems entspricht. Die fehlenden thermodynamischen Daten werden aus diesem Modell rekursiv ermittelt.
In beiden Fällen ist zu berücksichtigen, dass das Erzeugen optimierter Parameter keinesfalls deren Richtigkeit garantiert. Das vorgefundene Ergebnis ist vielmehr als das Optimum aus der Menge der berücksichtigten Daten anzusehen.
Die Anpassung der Parameter des thermodynamischen Modells an die experimentellen Werte erfolgt mit bekannten Routinen die dem Prinzip einer Kleinste-Fehlerquadrat-Prozedur folgen, z.B. mit dem Bayes-Algorithmus.
Zur Anpassung wird eine Fehlerfunktion als Differenz zwischen den ermittelten und den experimentellen Daten definiert. Die Fehlerfunktion hängt nur von den Parametern ab, die zur mathematischen Beschreibung des vorgegebenen thermodynamischen Modells erforderlich sind. Ziel der Anpassungsroutine ist das Auffinden der Modellparameter, die zum Minimum der Fehlerfunktion führen. In die Berechnung werden die Fehler der experimentellen Werte und die für die anzupassenden Modellparameter gesetzten Fehlergrenzen einbezogen.
Die Güte der optimierten Daten wird in der Regel anhand des Grades der Anpassung an experimentelle Daten oder der richtigen Wiedergabe eines bekannten Phasendiagramms abgeleitet. Diese Vorgehensweise ist streng genommen nur dann zulässig, wenn die zur Berechnung eingesetzte Datenbasis von den später angewandten Prüfkriterien unabhängig ist. Wird diese Bedingung nicht erfüllt, führen die Berechnungen zu falschen Daten. Um dies zu vermeiden, müssen unabhängige Kriterien als Prüfstein definiert werden, z.B. die richtige Berechnung eines untersuchten Reaktionssystems.
Eine einfache Erläuterung einer Optimierungsroutine
Zur Veranschaulichung des Prinzips der Optimierung dient das folgende stark vereinfachte Beispiel zur Ermittlung der Standardbildungsenthalpie einer festen, kongruent schmelzenden Verbindung. Die freie Enthalpiefunktion der festen Verbindung wird durch deren Standardbildungsenthalpie, Standardentropie und Wärmekapazitätsfunktion beschrieben:
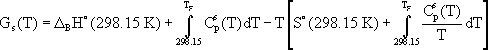
Die Beschreibung der geschmolzenen Verbindung mit gleicher Zusammensetzung erfordert zusätzlich zur freien Enthalpiefunktion die Schmelzenthalpie, die Schmelzentropie und die Wärmekapazität der flüssigen Phase.
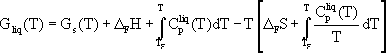
Beide Funktionen ergeben als Schnittpunkt den Schmelzpunkt der Verbindung. Ist die Standardbildungsenthalpie der festen Verbindung unbekannt, wird durch Einsetzen und Variieren von Startwerten für die fehlende Standardbildungsenthalpie der Verlauf der freien Enthalpiefunktion so lange verändert, bis aus dem Schnittpunkt mit der freien Enthalpiefunktion der Schmelze der richtige Schmelzpunkt der Verbindung resultiert. Die Schwierigkeit ist das Erreichen der Konvergenz der freien Enthalpiefunktionen.
Häufig kommen die freien Enthalpiefunktionen nur unter einem sehr kleinen Winkel zum Schnittpunke. Bereits geringste Veränderungen der Startwerte (ca. 1%) können ausreichen, um einen Schmelzpunkt bzw. eine andere thermodynamisch definierte Temperatur um mehrere 100 K zu verschieben (Fallbeispiel: Die Sensibilität thermodynamischer Modellsysteme).
Fallbeispiel: Die Gasphasensilicidierung von Chrom
Übergangsmetallsilicide können durch eine heterogene Reaktion eines Übergangsmetalls mit einem SiCl4/H2-Gasgemisch (Gl. 1) hergestellt werden.
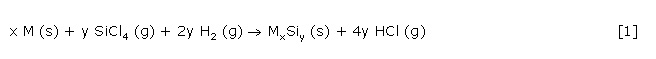
Diese Reaktion eignet sich zur eleganten Synthese phasenreiner polykristalliner Übergangsmetallsilicide, deren Stöchiometrie durch die Wahl der Reaktionsparameter Reaktionstemperatur und SiCl4/H2-Verhältnis sehr präzise eingestellt werden kann. Wesentlichstes Merkmal dieser Reaktion ist ihr streng thermodynamischer Verlauf, der auch die Nebenreaktion der Bildung eines Metallchlorides nach Gl. 2 umfasst.
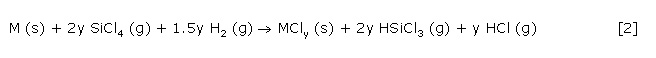
Im Unterschied zur Silicidbildung durch eine Festkörperreaktion der Elemente (reaktive Interdiffusion), die zur kinetisch kontrollierten Entstehung von Silicidphasen führt, kann während der Gasphasensilicidierung die Bildungskinetik der Gleichgewichtsphasen verfolgt werden.
Noch während der Silicidphasenbildung kommt es Bildung von Trichlorsilan (Gl.3). Diese setzt ein, sobald sich die unter den gegebenen Reaktionsbedingungen thermodynamisch stabile Silicidphase zu bilden beginnt.
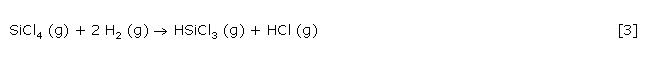
Reaktion 3 wird als die silicidphasenkatalysierte Hydrodechlorierung von Siliciumtetrachlorid zu Trichlorsilan bezeichnet. Die Gasphasensilicidierung eines Übergangsmetalls stellt dabei die erste Stufe der Hydrodechlorierung, die sogenannte Katalysatorformierung dar.
Eine thermodynamische Berechnung des Reaktionsverhaltens von Chrom im SiCl4/H2-Gasstrom zeigt das eine temperaturabhängige Konkurrenz zwischen Silicid- und Chloridbildung besteht. Bei tiefen Temperaturen kommt es thermodynamisch bedingt zur parallelen Bildung von Chrom(II)-chlorid und der chromreichsten Silicidphase Cr5Si3 (Gl. 4).

Mit zunehmender Temperatur wird CrCl2 reduziert und unmittelbar ins Silicid überführt.
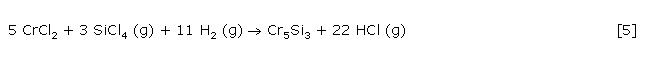
Sobald CrCl2 vollständig zu Cr5Si3 umgesetzt ist, beginnt die Konvertierung nach Gl. 3.
In diesem Fall bewirkt die Temperaturabhängigkeit der freien Standardbildungsenthalpie von CrCl2 die Chloridbildung ab ca. 670 °C. Gl. 4 und Gl. 5 stellen lediglich Teilreaktionen dar, die allgemein ausformuliert und addiert wieder zu Gl. 1 führen.

Fallbeispiel: Ein Beispiel für die Sensibilität thermodynamischer Modellsysteme
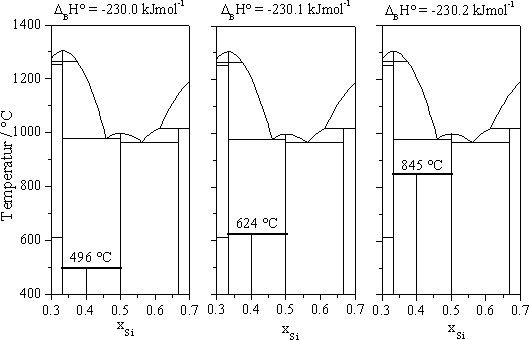
Am Beispiel der Phase Ni3Si2 kann die Robustheit bzw. Labilität der ermittelten freien Enthalpiefunktion verdeutlicht werden. Wird die für Ni3Si2 optimierte molare Standardbildungsenthalpie von 230.2 kJ×mol-1 nur geringfügig verändert, verschiebt sich die peritektoide Umwandlung der Phase um mehrere 100 K (Abb. 2). Das Beispiel verdeutlicht die Sensibilität wie "flach" das globale Minimum einer Phasengleichgewichtsberechnung ist, so dass geringste Veränderungen im Anstieg massive Auswirkungen auf die resultierende Reaktionstemperatur haben können. Das Beispiel veranschaulicht das Grundproblem jeder Optimierung, eine Konvergenz des Datensatzes zu erreichen.
Fallbeispiel: Mathematisch richtig ist nicht „chemisch“ richtig
In [Yan00] wird die Modellierung des Kupfer-Silicium-Phasendiagramms vorgestellt. Die Herausforderung dieses Systems liegt in der Komplexität des Phasendiagramms, den fehlenden Wärmekapazitätsfunktionen der Silicidphasen im gesamten Temperaturbereich und den zahlreichen widersprüchlichen Angaben zu deren Bildungsenthalpien. Die Berechnung nach [Yan00] baut deshalb im Wesentlichen auf gesicherten Daten zur Schmelze und den aus dem Phasendiagramm ableitbaren Informationen auf. Für die fehlenden Wärmekapazitätsfunktionen der festen Phasen wurden Funktionen nach der Neumann-Kopp-Regel verwendet.
De erstellte Datensatz gibt das Phasendiagramm korrekt wieder. Doch weist diese Arbeit eine entscheidende Besonderheit auf: Den für die Kupfersilicide angegebenen freien Enthalpiefunktionen liegen positive Standardbildungsenthalpien und positive Standardbildungsentropien zugrunde. Dies ist vor dem Hintergrund experimenteller Daten und dem generellen Trend der späten Übergangsmetallsilicide als unzutreffend einzustufen, obwohl einige experimentelle Arbeiten vorliegen, die eine positive Bildungsenthalpie angeben (Tab. 1). Zahlreiche weitere Untersuchungen [Köt02, Ack03b] und Untersuchungen an Cu-Si-Schmelzen [Wit94, Wit95] weisen eindeutig negative Bildungsenthalpien aus (Tab. 1).
Aus diesem Grund ist auch hier die richtige Wiedergabe des Phasendiagramms als mathematische Erfüllung der thermodynamischen Gleichgewichtsbedingungen anzusehen, ohne die thermodynamischen Eigenschaften der Kupfersilicide richtig zu beschreiben.
Tabelle 1: Molare Standardbildungsenthalpien und -entropien der Kupfersilicide.
Fallbeispiel: Die Direkte Synthese von Dimethyldichlorsilan
Die Reaktion zwischen Silicium und Methylchlorid in Gegenwart von Kupfer als Katalysator wird als die Direkte Synthese bezeichnet. Diese Reaktion, die unabhängig voneinander durch den Amerikaner Eugene G. Rochow (General Electric Company) und dem Deutschen Richard Müller in Radebeul entdeckt wurde, ist die Grundlage der heutigen industriellen Organosiliciumchemie, aus der alle heutigen bekannten Silikonprodukte hervorgehen.
Die häufig angegebene Reaktionsgleichung ist nur eine extrem vereinfachte Darstellung der realen Prozesse.

Tabelle 2 zeigt eine typische Produktverteilung der Direkten Synthese in Gegenwart eines Kupferkatalysators.
Tabelle 2: Typische Produktverteilung der Direkten Synthese [5]
Die Direkte Synthese ist eine kinetisch kontrollierte Reaktion, die nur weit entfernt vom thermodynamischen Gleichgewicht zu Dimethyldichlorsilan führt. Lediglich Kupfer ist in der Lage, das gewünschte Dimethyldichlorsilan in hohen Ausbeuten zu erzeugen. Die immer noch bestehenden Schwierigkeiten im Verständnis der Direkten Synthese beruht auf der Komplexität der Reaktion. Diese Komplexität entspringt der großen Anzahl von Faktoren (Temperatur, Druck, Katalysatormaterial, Promotoren, Katalysatorpräparation usw.), die Produkte sehr unterschiedlicher Zusammensetzungen und Ausbeuten führen können.
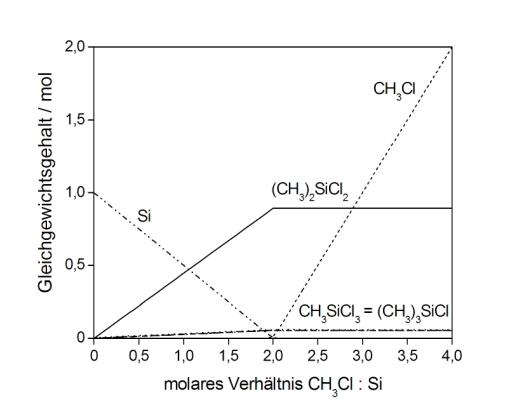
Thermodynamische Berechnungen können helfen, die ablaufenden Prozesse zu verstehen, indem die thermodynamischen Berechnungen unter Berücksichtigung kinetischer Hinderungen ausgeführt werden. Wird die Umsetzung von Silicium mit einer zunehmenden Menge von Methylchlorid berechnet, entstehen keinerlei Methylchlorsilane, sondern Siliciumterachlorid, als das stabilste Silan, und Trichlorsilan. Die Methylgruppe des Methylchlorides erleidet eine vollständige Spaltung in Wasserstoff, Methan und Kohlenstoff.
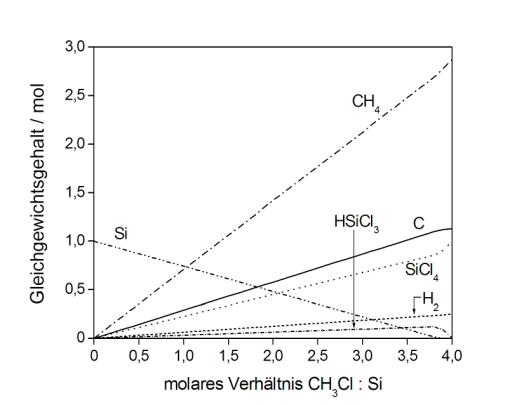
Werden kinetische Hinderungen in die Berechnungen eingeführt, resultiert eine Produktausbeute, die den experimentellen Befunden sehr gut entspricht. Mit dem so entwickelten Modell gelingt eine zuverlässige Modellierung der experimentell bestimmten Produktausbeuten in der Induktionsperiode der Reaktion und für die Reaktion in Gegenwart von variierenden Wasserstoffpartialdrücken. Weiterhin können Aussagen über den Einfluss des Reaktortyps und über Gleichgewichte zwischen den entstandenen Reaktionsprodukten getroffen werden.
| [5] | L.N. Lewis, W.V. Ligon, J.C. Carnahan, Silicon Chemistry 1 (2002) 23. |
