BTU auf einen Blick
Fakultät 3
Lehrstuhl Aerodynamik und Strömungslehre Prof. Dr.-Ing. Christoph Egbers

Fluid Mechanics

Spherical gap flow experiment

Inertial waves and Stewartson-layer instabilities in a librating and a differentially rotating spherical shell

Many planetary bodies consist of a solid inner and liquid outer core, e.g. Earth, Mercury, Jupiter, Earth's moon, Galilean moons, etc [1]. Most of them do not rotate at a constant speed but undergo forced background rotations, i.e. libration, a superposed periodic oscillation, and differential rotation. It is worth to know the interaction between the core rotation and the fluid's interior to understand e.g. tidal heating, fluid mixing or the generation of magnetic fields.

Inertial waves and Stewartson layers (as well as their instabilities) [2] are ubiquitous features in such rotating systems. Inertial waves arise due to an interaction between inertia and Coriolis forces. The Stewartson layer is a detached shear layer which compensates the angular-velocity differences between the inner and outer rotational part. An opportunity to investigate inertial waves and Stewartson layers is the spherical shell experiment. Recent experimental works have shown that inertial waves not only exist in librationally [3,4] or tidally [5] forced flows, but also in differentially rotating spherical shells [6,7].

Experimental set-up

The experiment (fig.1) [3,4] consists of an anodized aluminum inner sphere (rin=40mm) suspended on a shaft (1.4cm) inside an acrylic outer spherical shell (rout=120mm). The inner and outer sphere can rotate independently in the co- or counter-rotating direction. The gap between the spheres defines the area of investigation and is filled with low viscous silicone oil ν=0.65.

Figure 1: Set-up of the laser sheet and the spherical shell experiment with a meridional laser plane.

Two systems of rotation are considered: (i) inner sphere libration with Ωin(t)=Ω0[1+ε⋅sin(ωt)] and (ii) differential rotation (nominally spherical-Couette flow) where Ωin≠Ωout. The dimensionless Rossby number Ro=(Ωin-Ωout)/Ωout characterizes the strength of differential rotation. Here, ε with is the excitation amplitude and ω with 0≤ω≤2Ω0 is the excitation frequency of the inertial waves.

We use a laser-light-sheet technique to visualize the flow in the gap: (i) qualitatively in the meridional plane using Kalliroscope tracer particles (fig.1) and (ii) quantitatively in the horizontal plane in the rotating frame with the outer shell using spherical tracer particles.

Results

Inner sphere libration

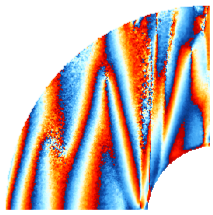
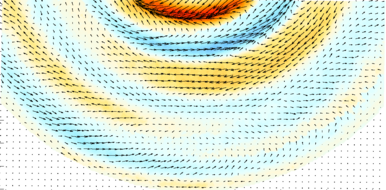
Linear inertial waves and Stewartson-layer instabilities excited by inner sphere libration have been discussed in detail in Hoff et al. (2016) [4]. An example for linear inertial waves is shown in figs.2a,b in the meridional (light intensities) and horizontal plane (velocities), respectively. Inner sphere libration gives rise to a Stewartson layer in the form of a prograde jet near the tangent cylinder (TC) at ri =40mm. We found that this layer becomes inertially unstable for libration amplitudes much larger than the libration frequency. As a consequence, a set of low-frequent Rossby waves is excited. These are either trapped near TC, drifting retrograde [4,8], or in the form of spiral waves, drifting prograde [4].

Negative differential rotation

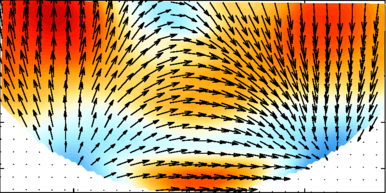
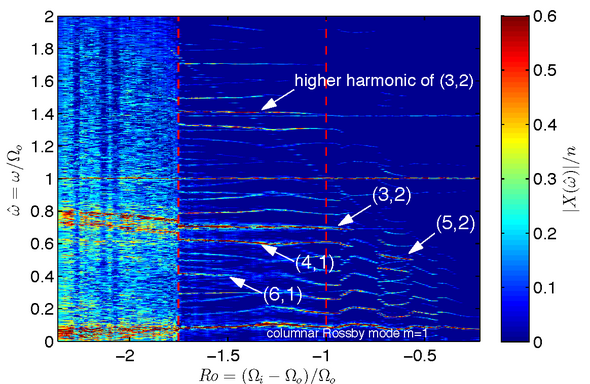
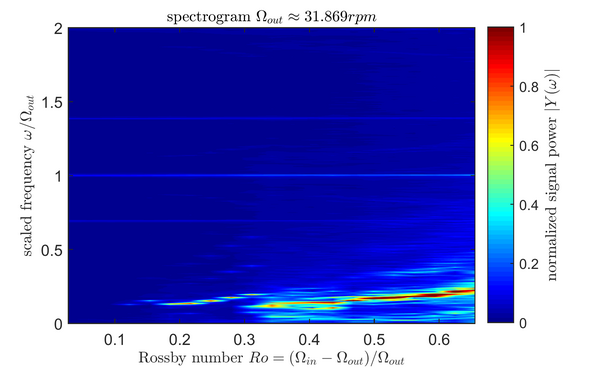
Recently, we are investigating inertial waves excited by differential rotation. Kelley et al. [6] and Rieutord et al. [7] found that inertial waves arise when the inner sphere rotates slower than the outer sphere or counter-rotates. Fig.2d shows a spectrogram of the azimuthal velocity as a function of Ro<0. The columnar Rossby mode is a result of the unstable Stewartson layer [8]. The labels mark frequency peaks corresponding to inertial modes with wavenumbers (l,m) [9]. The (3,2) mode, shown in fig.2c, is the most dominant mode. Its amplitude is increasing with decreasing Ro. This finally leads to a breakdown of the flow into small-scale disorder [10] at a critical Rossby number Rocrit. We found that Rocrit scales approximately with E1/5, where E is the Ekman number.

Positive differential rotation

When the inner sphere rotates faster than the outer sphere, the flow structure looks different compared to Ro<0. Fig.2e shows a corresponding spectrogram of the azimuthal velocity as a function of Ro>0. The first peaks occur due to the instability of the Stewartson layer [8]. In contrast to Ro<0, the instabilities are in the form of spiral waves, similar to the librationally-driven flow [4].

a)
b)
c)

a), b) Ω=24rmp, ωlib=0.4, εlib=0.4
c) Ωin=-42rpm, Ωout=64rpm, ω=0.705

d) Spectrogram for negative Rossby numbers
e) Spectrogram for positive Rossby numbers

Bibliography

  1. Spohn, T., Elsevier, 2nd edition, Amsterdam, 2007.
  2. Stewartson, K., J. Fluid Mech., 26, 131 - 144, 1966.
  3. Koch, S., Harlander, U., Egbers, Ch., Hollerbach, Fluid Dyn. Res. 45, 2013.
  4. Hoff, M., Harlander, U., Egbers, Ch., J. Fluid Mech., 789, 589 - 616, 2016.
  5. Favier, B., Barker, A. J., Baruteau, C., Ogilvie, G. I., MNRAS, 439, 845 - 860, 2014.
  6. Kelley, D. H., Triana, S. A., Zimmerman, D. S., Lathrop, D. P., Phys. Rev. E 81, 026311, 2010.
  7. Rieutord, M., Triana, S. A., Zimmerman, D. S., Lathrop, D. P., Phys. Rev. E 86, 026304. 2012.
  8. Hollerbach, R., J. Fluid Mech., 492, 289 - 302, 2003. Greenspan, H.P., Breukelen Press, Brookline, 1990.
  9. Kerswell, R. R., J. Fluid Mech., 382, 283 - 306, 1999.