Introduction

Thirty years ago it was observed that for many stars the emitted energy spectrum shows an extra bump in the infrared part. This infrared excess indicates a large gaseous disk encompassing the star. Such accretion disks are regions of planet formation (Fig.1a). Understanding the mechanisms that can result in an outward angular momentum transport is the central problem of planet formation, particularly in the theory of accretion disks. When a planet forms in a disk, angular momentum has to be carried away from the planet otherwise its rotation speed would be far too large. Only turbulence can achieve such a large angular momentum transport [1]. Accretion disks can be turbulent even in the absence of a magnetic field. Among other candidates the Stratorotational Instability (SRI) has attracted attention in recent years. The SRI is a purely hydrodynamic instability and much insight can be obtained from particularly designed laboratory experiments and numerical simulations in an axially-stratified Taylor-Couette setup [2, 3].

Experimental setup

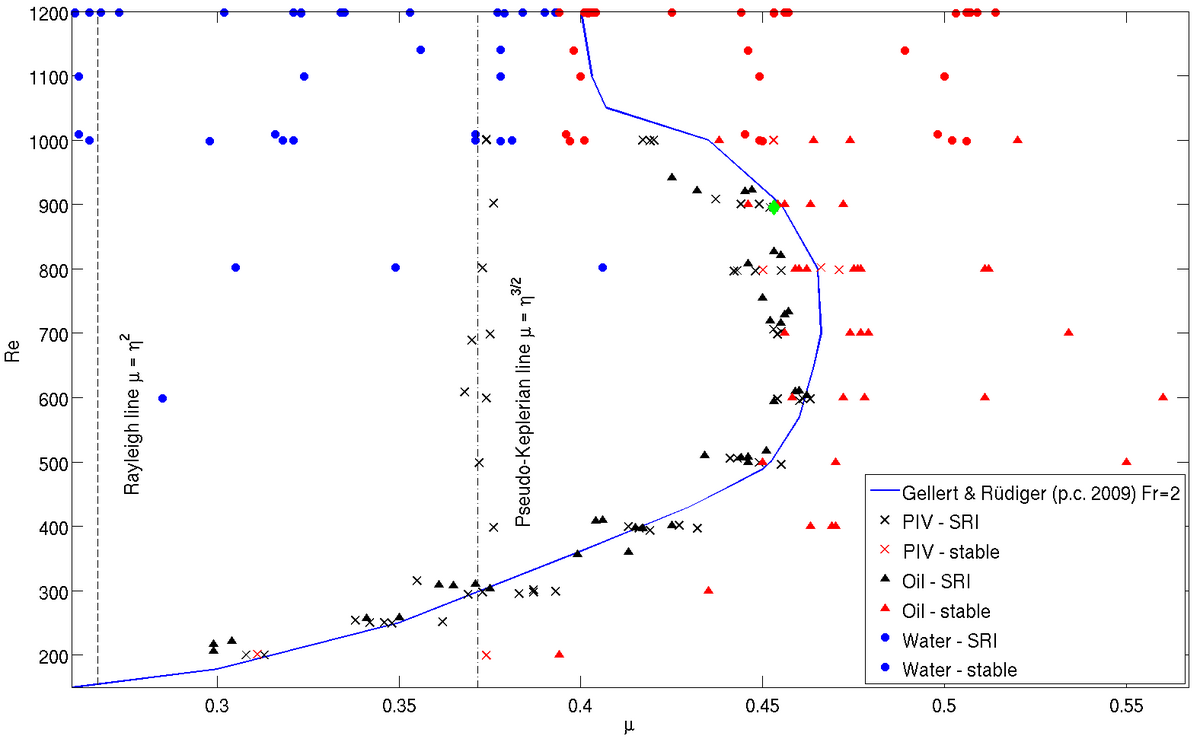
The SRI was experimentally studied by [4] using an axially salt stratified Taylor-Couette system. They found an excellent agreement with the linear stability analysis by [5] with respect to the course of the critical curve in a diagram spanned by the Reynolds number (Re) and the angular velocity ratio (μ). We use a Taylor-Couette apparatus (Fig.1b) where the fluid is axially stratified due to cooling the lower and heating the upper lid. Our system is three times as high as the one used by [4] and has a wider gap. We can reach Reynolds numbers between 3·10² and 3·10⁴. For Reynolds numbers < 10³ we use oil (Prandtl number 60) and for Reynolds numbers > 10³ we use water (Prandtl number 7). A co-rotating Particle Image Velocimetry system (PIV) gives us the opportunity to measure the flow in a horizontal and vertical plane simultaneously.

Results

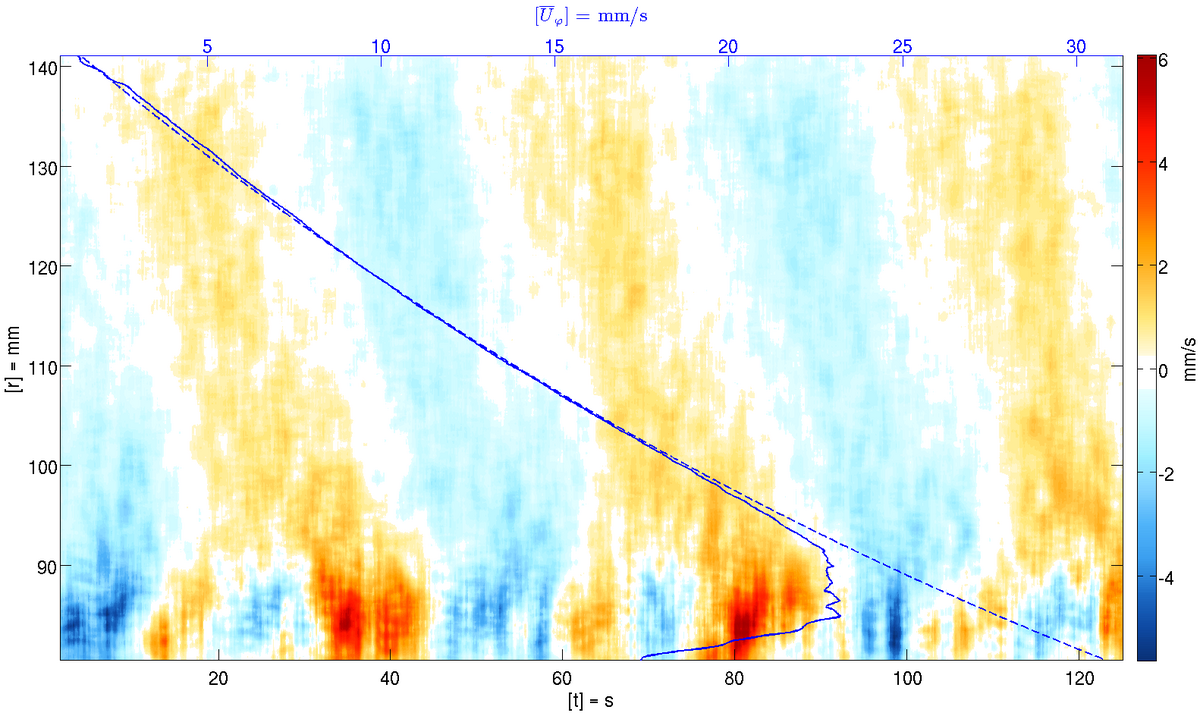
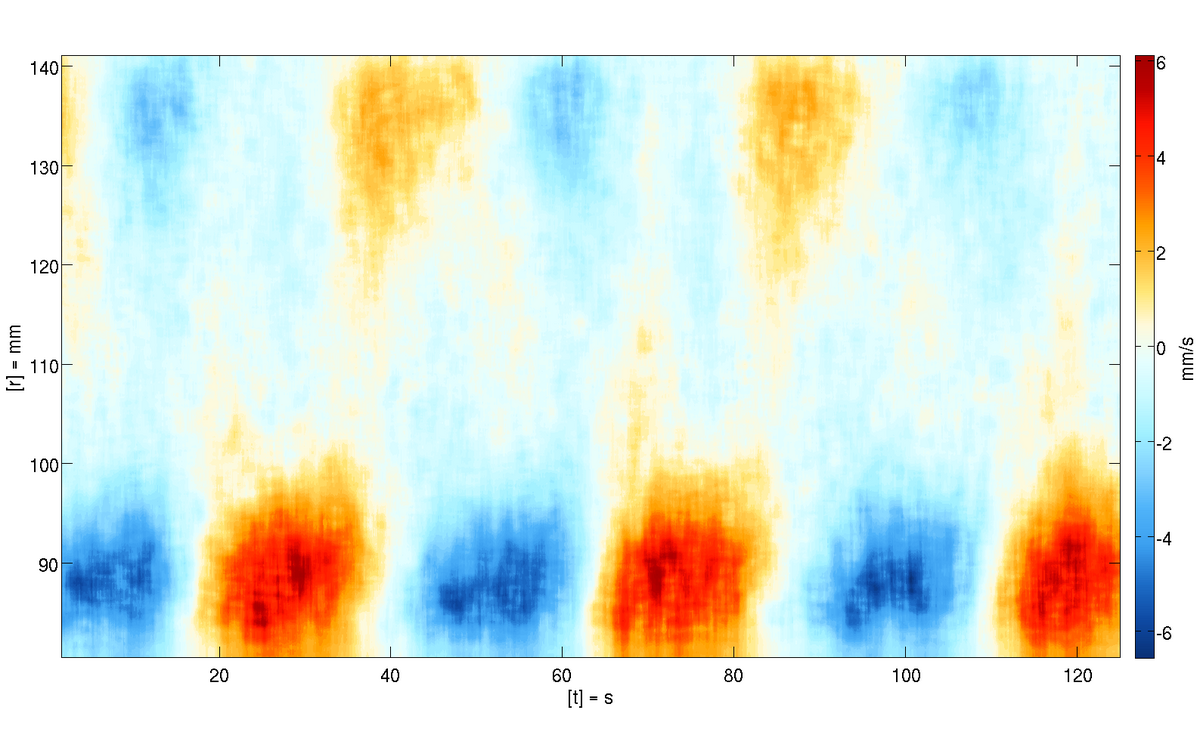
Like [4] we focus on the transition between axially symmetric flows and SRI modes in a μ−Re diagram (Fig.1c). In accordance with linear theory we find that for Re < 800 the critical curve approaches the line μ = η = 0.517, where η is the ratio between the radius of the inner and outer cylinder. However, for larger Re the curve bends backwards to smaller μ and approaches a line in between the Rayleigh line and the line μ = η. This backward bending is consistent with recent linear stability computations [6]. From this new findings it appears that the transition curves are more complicated as asumed e.g. in [4]. The experimental results are compared also with direct numerical simulations from two different numerical codes. Exemplary, Figure 2 shows space-time plots of the azimuthal and radial velocity component measured at Re = 900, μ = 0.453 (green diamond in Fig. 1c). The SRI is well established and oscillates with a period of 46s.

Bibliography

1. Armitage P. J. Planet Formation. Cambridge University Press, 2009.
2. Rüdiger G. et al. Magnetic Processes in Astrophysics. Wiley-VCH, 2013.
3. Gellert M. & Rüdiger G. J. Fluid Mech. 623:375-385, 2009.
4. Le Bars M. & Le Gal P. Phys. Rev. Lett. 99:064502, 2007.
5. Shalybkov D. & Rüdiger G. Astron. Astrophys. 438:411-417, 2005.
6. Rüdiger G. & Gellert M., personal communication