BTU auf einen Blick
Fakultät 3
Lehrstuhl Aerodynamik und Strömungslehre Prof. Dr.-Ing. Christoph Egbers

Fluid Mechanics

TEHD in cylindrical annuli: laboratory results

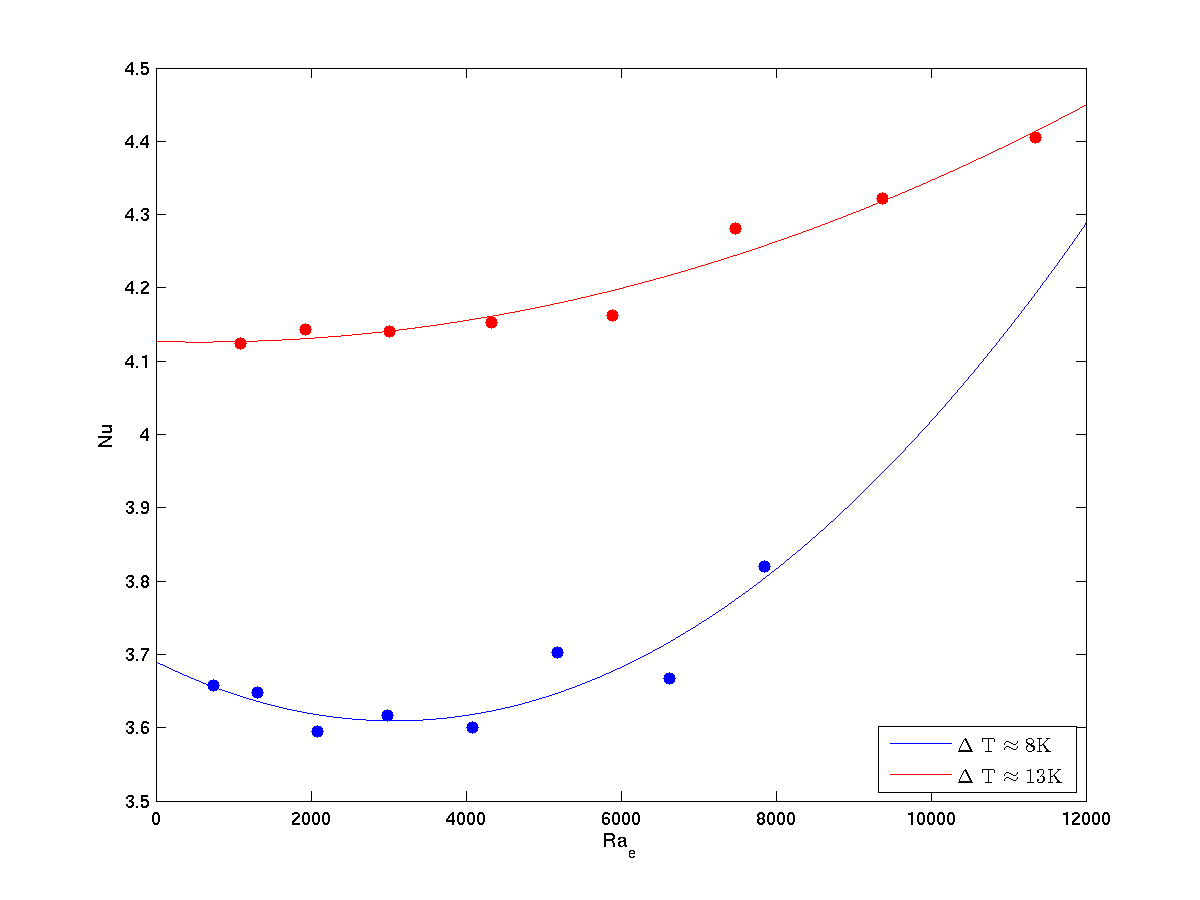
Consider a fluid-filled cylindrical enclosure with an inner heated cylinder of radius ri maintained at temperature Ti and an outer cooled cylinder of radius ro maintained at temperature To. The annulus is of height H with adiabatic top and bottom boundaries. The temperature difference DT = To-Ti induces natural convection in the gap width d = ro-ri at infinitesimal small increments of DT. This base flow experiences transition to instabilities depending on the radius ratio h= ri/ro, aspect ratio G = H/d, physical properties of the fluids (weighted with the Prandtl number) and on the driving force (weighted with the Rayleigh number). In this work here, we study the dielectrophoretic effect as heat transfer augmentation force via the performance of an alternating (a.c.) electric field superposing natural convection in the annulus experimentally. This procedure allows introducing an electric Rayleigh number for the system. Even though that dielectrophoretic effect has been neglected in comparison to dielectric (Coulomb) forces, that are driven by direct current (d.c.) electric fields, we are able to describe clear distortions of the base flow via flow visualization (shadowgraph). In addition, we quantify heat transfer via heating power measurements resulting in the determination of a Nusselt number for the inner cylinder. As already observed by Chandra and Smylie [1] and also described in [2] we observe a minimum of the Nu-numbers in the lower parameter domain of Rae. Up to now, an explanation for this damping of the heat transfer by the superposed electric field is missing. This behavior cannot be seen in the horizontal cell configuration case.

Bibliography

  1. Chandra, B. and Smylie, D. E. (1972). A laboratory model of thermal convection under a central force field. Geophysical Fluid Dynamics, vol. 3, pp. 211- 224.
  2. Dahley, N., Crumeyrolle, O., Futterer, B., Egbers, Ch., & Mutabazi, I. (2011). Parabolic flight experiment "Convection in a Cylinder" - Convection patterns in varying buoyancy forces. J.Phys.: Conf. Ser., vol. 318, p. 082003 (8pp).
  3. Dahley, N., Futterer, B., & Egbers, Ch., (2011). Control of convection by different buoyancy forces. 3rd Micro and Nano Flow Conference, Thessaloniki, Greece, 2011, Brunel, University Press, 2011, Hrsg.: T. Karayiannis, M. Collins, ISBN: 978-1-902316-98-7.
  4. Futterer, B., Dahley, B., & Egbers, C. (2013). Thermal electro-hydrodynamic heat transfer augmentation in vertical annuli exerting dielectrophoretic forces through a.c. electric field. Int. J. Heat Mass Transfer.
Figure 1: Development of the temperature on the outer cylinder. Increasing the voltage from 9kVpeak to 10kVpeak slightly increases the temperature on the outer wall (colors), while it slightly decreases the temperature on the inner wall (black line). The y-axis represents the height of the cylinder with six temperature measurement positions (No. 0 is at the bottom and No. 5 is at the top of the cell).
Figure 2: In the vertical cell the convective heat transfer (Nu) increases when the applied electric field is increased (Rae). The data points are taken at Vpeak=3, 4, 5, 6, 7, 8, 9 and 10kV at the indicated temperature difference between inner and outer cylinder. As already observed by Chandra and Smylie [1] and also described in [2] we observe a minimum of the Nu-numbers at low Rae. Up to now, an explanation for this behavior is missing.
Figure 3: Shadowgraph images of the flow inside the cells. Left row: no high voltage applied; right row: High voltage applied (7kV). While we see no change in the images of the horizontal cell, we observe a clear flow pattern change in the vertical cell even under 1g conditions in the laboratory when high voltage is applied.