Max Mengeringhausen (1903 – 1988) Erfindungen
Raumfachwerke. Anfänge, Grundlagen, Gesetzmäßigkeiten und Varianten
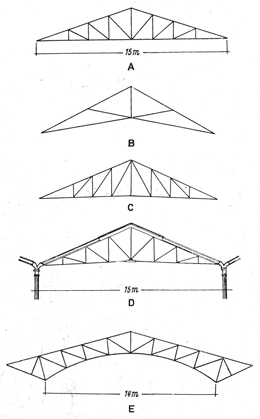
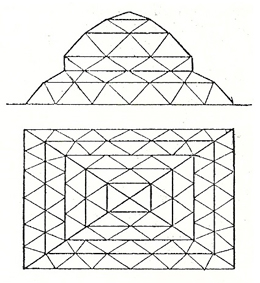
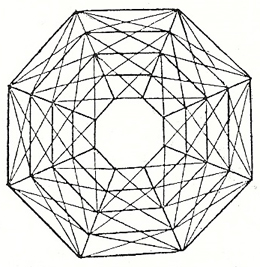
Die ersten Theorien über räumliche Fachwerke bauten auf die Konstruktionsweisen der ebenen Fachwerkbinder des 19. Jahrhunderts auf (siehe Abb. 4.01). Mengeringhausen erkannte, dass viele dieser ebenen Binder aufgrund unzureichender Horizontalaussteifung oder vernachlässigter Eigenschwingung konstruktive Mängel aufwiesen. Mit dem Beginn des Stahlhochbaus im 19. Jahrhundert gab es nur wenige Ingenieure, die das tatsächliche Verhalten von Stabverbänden im Raum erforschten. August Föppl (1854-1924) war einer dieser wenigen. Durch den Einsturz der Birs-Brücke bei Mönchenstein (heute: Münchenstein), Kanton Basel-Landschaft, Schweiz sah sich Föppl animiert, seine Erkenntnisse über räumliche Fachwerke zu veröffentlichen, um weiteren baufachlichen Fehlern dieser Art entgegenzuwirken. In den 1880er Jahren erschienen seine ersten Artikel über Raumfachwerke. 1892 informierte Föppl in seinem Werk „Das Fachwerk im Raume“ unter anderem über seine Studien zu den sogenannten Netzwerkkuppeln, welche durch Anordnung von Dreiecken statisch stabil sind (siehe Abb. 4.02). Dies war ein wichtiger Schritt für die Entwicklung erster räumlicher Kuppelkonstruktionen im Stahlhochbau. Er verglich die Netzwerkkuppel zum Beispiel mit der Schwedlerkuppel, deren Felder durch schlaffe Diagonalen ausgekreuzt sind (siehe Abb. 4.03). [MENGERINGHAUSEN 1975, S. 14-17] Mengeringhausen würdigt die Leistung Föppls in seinem eigenen Werk „Komposition im Raum“ mit den Worten, August Föppl habe „die Grundlagen einer Systematik, neue statische Gesetze und für eine Reihe wichtiger Bauformen klare Begriffe geschaffen“. [MENGERINGHAUSEN 1975, S. 17]



In der Zeit zwischen den beiden Weltkriegen bestand im Bauwesen die Forderung nach einheitlichen Systemmaßen, um serienmäßig und folglich schnell und effizient produzieren zu können. Damit wurden schon beim Gebäudeentwurf neue Maß- und Ordnungsverhältnisse notwendig, wie auch Ernst Neufert (1900-1986) 1936 in seiner Bauentwurfslehre erklärte. Außerdem orientierte sich Mengeringhausen an den Aussagen des Architekten Walter Gropius (1883-1969) über die „zukünftige Baukunst“. Gropius ging davon aus, dass man durch die vielfältige Montagemöglichkeit genormter, seriell gefertigter Bauteile verschiedenartige Gebäudetypen errichten könne. Diesen Umständen entsprechend setzte sich Mengeringhausen 1939 persönlich zum Ziel, ein Maßsystem mit Elementen zu entwickeln, welche durch genormte Baulängen serienmäßig, industriell herstellbar und für Gebäude verschiedenster Funktionen einsetzbar sind. Außerdem sollte eine nachträgliche Erweiterung und Umgestaltung der Tragelemente möglich sein. [MENGERINGHAUSEN 1975, S. 20]
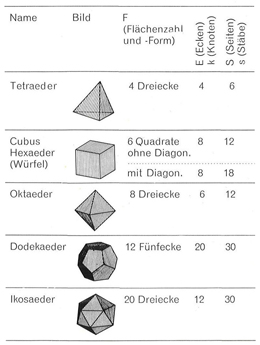
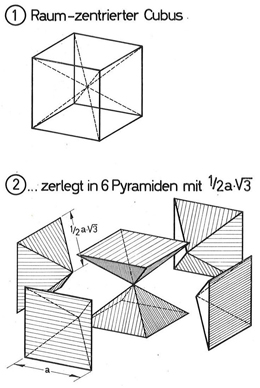
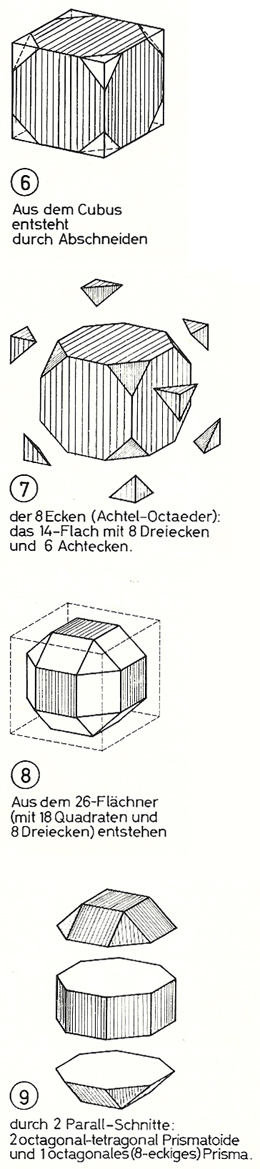
Auf der Grundlage der Studien von August Föppl (1854-1924) sowie der geometrischen Stereometrie nach Karl Heinze definierte der Maschinenbauingenieur bestimmte Grundbausteine, welche in ihrer Zusammensetzung besonders günstig für die Erzeugung räumlicher Tragwerke sind. Die Aspekte, auf denen Mengeringhausens Forschungen aufbauten, werden im Folgenden erläutert: Besonders wichtig war zum einen die Untersuchung und statische Bewertung der fünf platonischen Körper durch Föppl. Platonische Körper sind regelmäßige Vielflächner mit deckungsgleichen Flächen und identischen Seitenlängen (siehe Abb. 4.04). Tetraeder, Oktaeder und Ikosaeder sind als Körper mit Dreiecksflächen statisch stabil. Kubus und Dodekaeder erreichen diesen Status durch entsprechende Auskreuzungen der Seitenflächen. Um die statische Bestimmtheit der Platonischen Körper bewerten zu können, entwickelte August Föppl (1854-1924) Stabilitätsbedingungen in Abhängigkeit von der Anzahl der Stäbe und Knoten. Für ebene Fachwerke gilt die Gleichung: 2k - s = 3. Für Raumfachwerke gilt: 3k - s = 6, wobei k der Anzahl der Knoten und s der Anzahl der Stäbe entspricht [MENGERINGHAUSEN 1975, S. 28]. Zum anderen sollten nicht ausschließlich die oben genannten fünf Grundkörper, sondern auch davon abgewandelte Elemente zur Bildung von Raumfachwerken dienen. Mengeringhausen orientierte sich dafür an der genetischen Stereometrie, ein mathematisches Prinzip zur Zerlegung und Bildung komplizierter Körper zu bzw. aus einfachen Körpern. Die Basis dafür schuf der Ingenieur und Mathematiker Karl Heinze im 19. Jahrhundert. Beispielsweise zeigte er, wie man einen raumzentrierten Kubus in sechs Pyramiden zerlegen kann (siehe Abb. 4.05). Bei einem raumzentrierten Kubus liegt das Zentrum in der räumlichen Mitte des Körpers. Auch der 26-flächige Körper, der Mengeringhausen als geometrische Struktur für seinen „MERO-Universal-Knoten“ diente, war ein Bestandteil der Studien von Heinze (siehe Abb. 4.06). Dieser Körper war sogar bereits dem Mathematiker Archimedes (285 v.Chr. - 212 v.Chr.) bekannt. [MENGERINGHAUSEN 1975, S. 26-28 und 71]
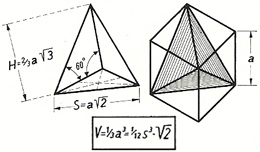
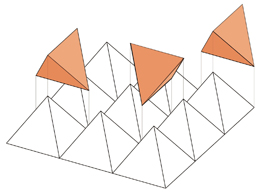
In seinem Buch „Komposition im Raum. Raumfachwerke aus Stäben und Knoten“ veranschaulicht Mengeringhausen seine eigenen stereometrischen Überlegungen (siehe MENGERINGHAUSEN 1975). Größtenteils ging er dabei wie Karl Heinze von dem Kubus aus und versuchte durch verschiedene Schnittführungen die Platonischen Körper oder davon abgewandelte Körper zu erzeugen. Abb. 4.07 zeigt einen Tetraeder, welcher durch entsprechende Schnittführung in einen Kubus eingeschrieben ist. Das sogenannte „Vierflach“, ein Körper mit vier Dreiecksflächen, ist generell der kleinste zu erzeugende Elementarkörper innerhalb seiner Studien. Der Tetraeder ist dabei mit seinen sechs gleichlangen Stäben bzw. Kanten ein regelmäßiges Vierflach. Die beiden weiteren Vierflächner sind das Achteloktaeder (ein gleichseitiges Dreieck, drei rechtwinklige Dreiecke) und das Vierteloktaeder (zwei gleichseitige, zwei rechtwinklige Dreiecke) (siehe Abb. 4.08). Der Tetraeder gemäß der Abbildung 4.07 entsteht durch „Abschneiden“ von vier Achteloktaedern von einem Kubus. Die Tetraederform findet bei der Umsetzung von Raumfachwerken häufig Anwendung. So besteht bspw. der Pavillon der Siemens-AG für die Deutsche Industrie-Ausstellung von 1971 in São Paulo, Bundestaat São Paulo, Brasilien grundsätzlich aus zwei, sich anschmiegenden Tetraedern. Zur Ausbildung des Raumfachwerks sind diese Grundkörper wiederum in einzelne kleine Tetraeder unterteilt (siehe Abb. 4.09). Ein anderer von Mengeringhausen gern verwendeter Körper war das Oktaeder und seine Zerlegungsformen Halboktaeder und Achtel-Oktaeder. Die beiden zuletzt genannten Formen wurden als Elementarkörper für die Konstruktion des Messepavillons „Salon Antiquaries“ in Paris in 1966 (siehe Abb. 4.10) oder die Station der Ausstellungsbahn der „Internationalen Verkehrs-Ausstellung“ in München in 1965 (siehe Abb. 4.11) verwendet. [MENGERINGHAUSEN 1975, S. 30-41]
Anhand seiner Studien stellt Mengeringhausen verschiedene Regeltypen für Raumfachwerke auf. Diese setzen sich aus einer Auswahl der stereometrischen Grundkörper, meistens jedoch aus dem Tetraeder und Oktaeder zusammen. Diese beiden Grundelemente lassen sich gut kombinieren [MENGERINGHAUSEN 1975, S. 28 und 46-59]. Abb. 4.12 zeigt einen Regeltypus, welcher sich aus dem Tetraeder und dem Halboktaeder zusammensetzt. Das Raumfachwerk der Halle der „Stadt von morgen“ auf der Interbau Berlin wurde im Jahre 1957 nach diesem Regeltypus erbaut [MENGERINGHAUSEN 1975, S. 129]. Die Abb. 4.12 verdeutlicht mit „½ O + T“ außerdem Mengeringhausens Regel, seine Raumfachwerke mit Kürzeln zu benennen. Die verwendeten stereometrischen Körper werden durch ihren Anfangsbuchstaben abgekürzt. Dies ähnelt den Benennungsregeln der Chemie [MENGERINGHAUSEN 1975, S. 45].
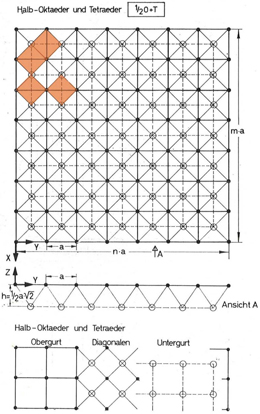
In den acht Baugesetzen für Raumfachwerke beschreibt Mengeringhausen sinngemäß folgendes:
- Das Hauptprinzip besteht darin, Raumfachwerke aus gleichseitigen und gleichschenkligen Dreiecken so zusammenzusetzen, dass regelmäßige Vielflächner entstehen.
- Der Einsatz gleicher Stablängen und einheitlicher Knotenstücke ermöglicht eine industrielle, serienmäßige Produktion. Außerdem weisen die Raumfachwerke aufgrund ihrer Regelmäßigkeit statisch optimale Verhältnisse auf.
- Die Normung der Fachwerkstäbe gelingt durch die Definition von Maßreihen mit dem Wachstumsfaktor √2.
- Mit verschiedenen Stablängen der geometrischen Reihe kann ein Gefüge aus ähnlichen, regelmäßigen Polyedern konstruiert werden.
- Die Größe der Oberflächen bildet eine geometrische Reihe mit dem Faktor 2. Dies gilt entsprechend für die Rauminhalte mit dem Faktor 2 √2.
- Alle Elementarkörper in Form von platonischen Körpern und deren Abkömmlinge können aus genormten Stäben gebildet und mit einem einzigen Universalknotenstück verbunden werden.
- Dieses Knotenstück ist ein 26-flächiger Körper.
- Regelmäßige Raumfachwerke können ausschließlich mit MERO-Normknoten, sprich dem 26-flächigen Universalknotenstück mit 18 Anschlussmöglichkeiten verbunden werden.
Mengeringhausens regelmäßige Raumfachwerke zeichnen sich außerdem dadurch aus, dass ausschließlich platonische Körper als kleinste Elementarkörper sowie Stablängen der Maßreihen mit dem Wachstumsfaktor √2 für die Bildung der räumlichen Tragwerke verwendet werden. Auch die Größe der DIN-gerechten Papierformate wurde mithilfe des Faktors √2 nach den Grundlagen von Walter Porstmann (1886-1959) entwickelt.
[MENGERINGHAUSEN 1975, S. 43-45]
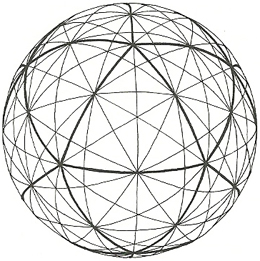
Ein weiterer Ingenieur, welcher sich wie Mengeringhausen mit dem Konstruieren auf Grundlage von geometrischen Strukturen beschäftigte, war Richard Buckminster Fuller (1895-1983) mit seinen geodätischen Kuppeln. Dabei ging er von dem Ikosaeder, dem regelmäßigen Platonischen Körper mit 20 gleichseitigen Dreiecken aus und projizierte dieses auf eine Kugel. Dadurch entstanden aus den gleichseitigen Dreiecken sphärisch gekrümmte Dreiecke. Diese unterteilte Fuller mithilfe ihrer Mittelsenkrechten und konnte somit ein System aus einheitlichen Stablängen für Kuppelkonstruktionen erzeugen. Die Entwicklungen der geodätischen Kuppeln dürften zeitgleich zu den Studien der Raumfachwerke von Mengeringhausen entstanden sein. 1954 wird Fullers Patent auf diese Kuppeln stattgegeben. Seit Ende der 1950er Jahre wird diese Art von Kuppeln bspw. für Einhausungen von Radargeräten verwendet.
[KURRER 2004a, S. 615-616]
Mengeringhausens genutzte Technologien und Erfindungen.
Die folgende Liste ist nur ein Auszug aus den über 350 eingereichten Patenten Mengeringhausens; abweichend hierzu beziffert Karl-Eugen Kurrer in seinem Stahlbau-Artikel „Zur Komposition von Raumfachwerken von Föppl bis Mengeringhausen“ die Menge an Mengeringhausens Patenten mit „nur“ „über zweihundert“ [KURRER 2004b, S. 93]. Viele dieser Patente beantragte Max Mengeringhausen sowohl in Deutschland als auch international. Als Beispielländer können Österreich und die Schweiz angeführt werden. Einige spätere Patente wurden von seiner Firma MERO entwickelt. Über DEPATISnet, dem Online-Recherche-Portal des Deutschen Patent- und Markenamtes lassen sich sowohl ein Gesamtüberblick als auch detaillierte Einblicke der Patente Mengeringhausens gewinnen.
| Anmeldedatum | Patentbeschreibung | Weitere Informationen |
|---|---|---|
| 22.01.1932 | Vorrichtung zur Beseitigung von Strömungsgeräuschen in Wasserleitungen. | Patent-Nr.: DE000000609738A. Patent-Anmelder: Max Mengeringhausen. |
| 13.10.1933 | Drosselvorrichtung zur Beseitigung von Strömungsgeräuschen. | Patent-Nr.: DE000000620123A. Patent-Anmelder: Max Mengeringhausen. |
| 22.07.1933 | Geräuschdämpfendes Drossel- und Absperrorgan für Flüssigkeitsleitungen. | Patent-Nr.: DE000000632394A. Patent-Anmelder: Max Mengeringhausen. |
| 30.10.1936 | Rohrverbindung. | Patent-Nr.: DE000000708224A. Patent-Anmelder: Max Mengeringhausen. |
| 17.01.1939 | Rohrmuffenverbindung. | Patent-Nr.: DE000000720239A. Erfinder: Bruno Engel & Max Mengeringhausen. Patent-Anmelder: Max Mengeringhausen. Dieses Patent ist vermutlich als Mengering-Doppeldichtung bekannt geworden (siehe Abb. 2.04). Erfunden wurde die Doppeldichtung bereits 1937/ 1938. |
| 12.03.1943 | Verbindung von Rohrstäben und knotenbildenden Verbindungsstücken, insbesondere für zerlegbare Fachwerkkonstruktionen. | Patent-Nr.: DE000000874657B. Patent-Anmelder: Max Mengeringhausen. Hinter diesem Patent verbirgt sich die Mengeringhausen Rohrbauweise, die unter dem Namen MERO bzw. MERO-Bauweise weltberühmt wurde. Mengeringhausen entwickelte dieses Tragsystem bereits 1942. Ein Jahr später erhielt er darauf im Deutschen Reich das hier gelistete Patent, welches schließlich 1953 zu BRD-Zeiten vom Patentamt neu anerkannt wurde. |
| 24.01.1950 | Fertigkonstruktion für Installationsanlagen. | Patent-Nr.: DE000000852755B. Patent-Anmelder: Max Mengeringhausen. |
| 01.06.1967 | Halterung und Deckendurchführung von Rohrpaketen zur Fertiginstallation. | Patent-Nr.: DE000001600522A. Patent-Anmelder: Max Mengeringhausen. |
| 21.11.1969 | Verfahren und Vorrichtung zur Herstellung von Stabelementen, z.B. für Raumfachwerke. | Patent-Nr.: DE000001958392A. Patent-Anmelder: Reinhold Gehrig, Max Mengeringhausen, Hermann Quenzel und Willi Spanheimer. |
| 14.06.1975 | Gebäudekonstruktion mit einem Raumfachwerk aus Stäben und Knotenstücken mit z.B. die Gebäudeaußenhaut bildenden Platten. | Patent-Nr.: DE000002559750A1. Pate |
Mengeringhausens genutzte Technologien und Erfindungen. Kommentierte Erfindungen
Die „MEngeringhausen ROhrbauweise“ wird größtenteils abgekürzt und entsprechend als MERO-Bauweise bezeichnet [KURRER 2004a, S. 616]. Mengeringhausen entwickelte sie bereits im Jahr 1942. Noch im selben Jahr brachte er eine Veröffentlichung zu dieser heraus, bevor er schließlich am 12.03.1943 das Patent dazu erhielt. Grundsätzlich werden zur Errichtung der räumlichen MERO-Tragwerke ausschließlich 2 Konstruktionselemente, nämlich Rohrstäbe und Knoten aus Stahl verwendet. Werden Konstruktionen möglichst geringen Gewichts angestrebt, verwendet man Leichtmetalle wie z.B. Aluminium. Tragwerke, welche geringen Beanspruchungen ausgesetzt sind, können auch mit farbigen Kunststoffrohren ausgeführt werden. Die Bauteile ermöglichen ein schnelles (De-) Montieren und verfügen über ein geringes Eigengewicht, was den Transport erleichtert. Die MERO-Raumfachwerke eignen sich besonders für einen schnellen Auf- und Abbau und werden vor allem für den Bau von Gerüsten, Messe- und Ausstellungshallen, Podien und Tribünen eingesetzt. Montierte Rohrstäbe und Knoten bilden einen steifen Anschluss, wirken statisch dennoch wie ein Gelenk.
[MENGERINGHAUSEN 1975, S. 66-68]
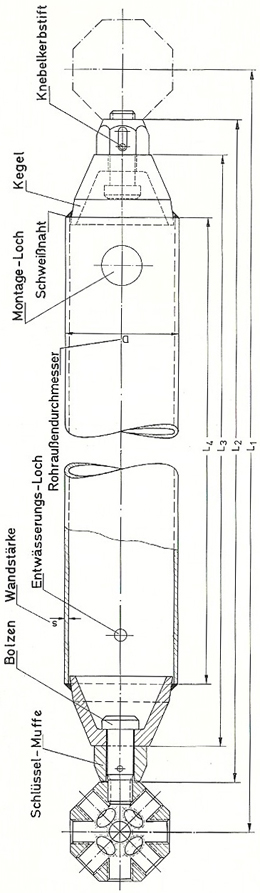
Die Längsachsen der Stäbe schneiden sich genau im Knotenmittelpunkt. Die Rohrstäbe besitzen an beiden Enden Gewindekupplungen zum konzentrischen Anschluss an die Knoten. Dadurch können Zug- und Druckkräfte entlang der Stab-Längsachse in das Zentrum des Knotens eingeleitet werden. Die Verbindung erfolgt durch einen Schraubanschluss. Dementsprechend ist ein Kreisringquerschnitt für die Rohrstäbe passend. Das kegelförmige Endstück des Stabes enthält einen Gewindebolzen. An diesem ist ein Mitnehmerstift, auch als Knebelkerbstift bezeichnet, befestigt. Der Stift greift in den Längsschlitz der Muffe ein. Da der Längsschlitz wie ein Langloch wirkt, kann sich der Gewindebolzen beim Drehen der Muffe mitdrehen. Auf diese Weise wird der Bolzen in das Knotenstück geschraubt und kann auf diese Weise ebenso wieder gelockert werden (siehe Abb. 4.15). Zunächst entwickelte Mengeringhausen nur MERO-Bauteile mit den Gewindegrößen M12 und M20. Seit Ende der 1960er Jahre finden auch andere Gewindegrößen Anwendung [KURRER 2004a, S.619]. Der Korrosionsschutz wird durch eine Feuerverzinkung der Stäbe gewährleistet. Dies ist insbesondere bei außenliegenden Konstruktionen wichtig. Raumfachwerke aus Aluminium werden durch das Eloxalverfahren geschützt [SCHOLZ/ HIESE/ MÖHRING 2011, S. 553]. Dabei wird durch chemische Elektrolyse mit Schwefel- und/ oder Oxalsäure eine harte, abriebfeste Oxidationsschicht ausgebildet. Um eine gestalterisch schönere Wirkung zu erreichen, können die Stäbe außerdem lackiert oder mit Kunststoff beschichtet werden. Die Stäbe verfügen über ein Montageloch, um die Gewindebolzen gegebenenfalls nachträglich auswechseln zu können. Außerdem ist pro Stab mindestens ein Entwässerungsloch vorgesehen. Bei Raumfachwerken im Freien werden die Montagelöcher durch Gummidichtungen verschlossen.
[MENGERINGHAUSEN 1975, S. 68-69]
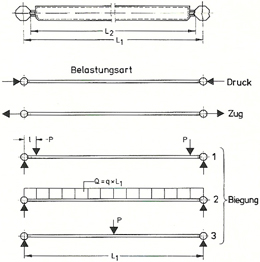
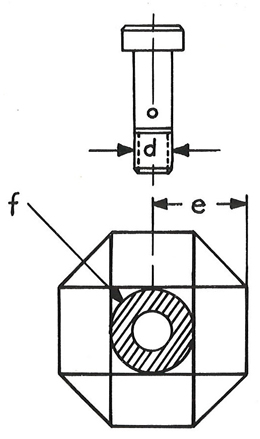
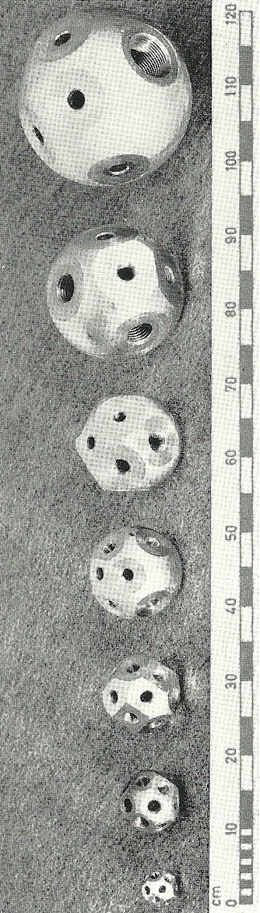
Die Knotenstücke sind nur mathematisch gesehen Polyeder, denn in der Praxis werden die Ecken abgerundet. Pro Quadratfläche ist ein Innengewinde mittig angeordnet, sodass eine einwandfreie Kraftübertragung der konzentrisch gerichteten Zug- und Druckkräfte aus den Stäben erfolgen kann. Die Polyederflächen sind orthogonal zum Innengewinde und zu den Stabachsen. Die Zugkraftübertragung wird durch den Gewindebolzen sichergestellt. Die Größe der übertragenen Kraft ist dabei von der Größe des Gewindedurchmessers „d“ abhängig (siehe Abb. 4.17). Die Druckkraftübertragung erfolgt von der Schlüsselmuffe auf die Polyederfläche, wobei die Größe der übertragenen Kraft von der Größe der Auflagefläche „f“ der Muffe abhängt. Die Stäbe können neben Normalkräften auch Querkräfte geringen Maßes wie bspw. Personenlasten während der Montage aufnehmen. Das heißt, die Stäbe können auch auf Biegung beansprucht werden (siehe Abb. 4.16). Das Systemmaß „L1“ entspricht dem Abstand von Knotenmitte zu Knotenmitte. Der Abstand „e“ gibt den Abstand der Polyederflächen vom Knotenmittelpunkt in der Achse des Innengewindes sowie des anschließenden Stabes an. Dieses Maß ist vom größten Gewindemaß „d“ abhängig und sehr wichtig für die Bemessung der Stablängen (siehe Abb. 4.17).
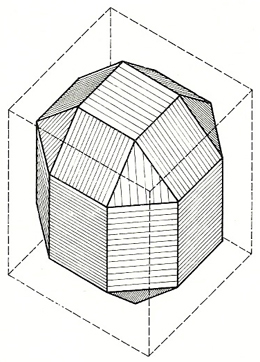
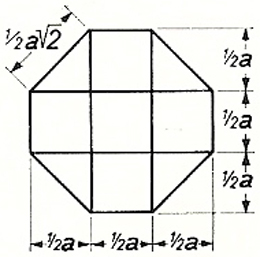
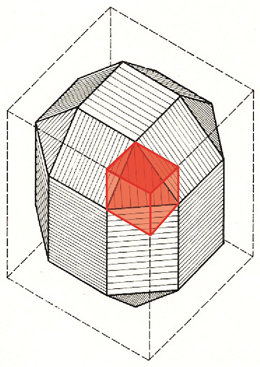
Der „MERO-Universal-Knoten“ entspricht dem geometrischen Modell eines 26-flächigen Körpers, dessen Geometrie so wie bei vielen anderen Körpern Mengeringhausens vom Kubus abgeleitet ist (siehe Abb. 4.18). Dieser Körper enthält 18 Quadrate und 8 gleichseitige Dreiecke und verfügt insgesamt über 13 Achsen. Die Quadratflächen entstehen durch das Abtrennen halber Quadrate (siehe Abb. 4.19). Um schließlich die Dreiecksfläche des Knotens zu erhalten, muss wiederum ein Quadratsegment bestehend aus 3 rechtwinkligen Dreiecksflächen sowie einer Quadratfläche entfernt werden (siehe Abb. 4.20).
Bei den meisten Raumfachwerken werden jedoch nicht alle Anschlüsse des „MERO-Universal-Knotens“ benötigt. Meistens kommt der MERO-Normknoten des flächenzentrierten Kubus zur Anwendung. Bei dem flächenzentrierten Kubus erhält man das Zentrum aller sechs Flächen, indem man diese durch Diagonalen auskreuzt. Das Tetraeder ist ein Beispiel für einen Körper, welcher nach Mengeringhausen aus einem flächenzentrierten Kubus gebildet wird (siehe Abb. 4.07). Wird ein Tetraeder zur Bildung eines Raumfachwerkes verwendet, wird der MERO-Normknoten als Verbindungsmittel genutzt. Der Körper entspricht ebenso der mathematischen Geometrie des 26-flächigen Körpers, wobei aber nur 9 Achsen durch die Mittelpunkte der 18 Quadrate für die Krafteinleitung genutzt werden. Das heißt, alle 18 Quadrate sind mit einem Innengewinde versehen. Die Hauptachsen x, y, z sind orthogonal. Die Nebenachsen schließen mit einem Winkel von 45° an das System an (Vgl. Projekt Halle der „Stadt von morgen“, Interbau, Berlin, 1957).
Mengeringhausen erfand des Weiteren verschiedene Sonderknoten für Stäbe, welche nicht unter einem 45°-Winkel an den Knoten anschließen. Dadurch wird eine variable Gestaltung der Raumfachwerke ermöglicht. Die vier rechten (bzw. oberen) Knoten der Abb. 4.21 zeigen eine Auswahl solcher Knoten. Bis heute wurden von der Firma MERO je nach Anwendungsgebiet eine Vielzahl verschiedener Knoten entwickelt.
[MENGERINGHAUSEN 1975, S. 69-74]
