GeoFlow II
Numerics
It is mostly desirable to have preliminary numerical simulations to find out the significant parameter range for the GeoFlow2 experiments. The governing equations are modeled in the Boussinesq approximation, which is valid for the expected fluid velocity of the Newtonian working fluid called 1-Nonanol.
In contrast to traditional simulation work for mantle dynamics the Prandtl number (Pr) for our experiment is reasonable high (Pr=125 to Pr=185). Since the Prandtl number influence on the fluid flow is logarithmic, we do not expect significant differences between Pr=185 and an Earth's mantle Prandtl number of Pr=1023. In the following we present the equations:
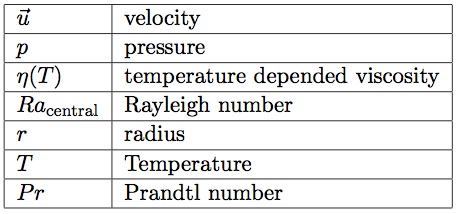
\[\nabla \cdot \vec{u}= 0\]
\[Pr^{-1} = {\left[ {\partial \vec{u} \over \partial t} + (\vec{u} \cdot \nabla) \vec{u}\right]} \\= - \nabla p + \nabla \cdot (\eta (T) (\nabla \vec{u} + (\nabla \vec{u}^T)) + Ra_{central} {{T} \over {r^5}} \vec{e_r}\]
\[{\partial{T} \over \partial{t}} + \vec{u} \cdot \nabla T = \Delta T\]
\[\eta (T) = \eta_{ref} \exp{(-E(T-T_{ref}))}\]
The first equation is the mass conservation, in terms of a divergence free velocity field. The second one is the well known Navier-Stokes equation, herewith an applied dielectrophoretic force field. In contrast to the first mission the viscosity depends on the local temperature and changes the formally linear viscosity term into a non-linearity. The temperature equation closes the set of equations.
Due to the special spherical geometry of the experiment the equations are solved with a pseudo-spectral method developed by R. Hollerbach and extended at the BTU. The used method is fast and accurate for linear problems. In order to solve the non-linear thermo-viscous term of the Navier-Stokes equation, a real space transformation is applied, which decreases the overall speed. This special type of solution is much more complicated, but necessary for the GeoFlow2 mission.